SOLUTION: Find the center and radiu of the circle and sketch its graph. {{{x^2+y^2}}} = {{{25}}}

You have to learn the standard equation 
for a circle.

That is, you must memorize that

(x - h)² + (y - k)² = r²

is the equation of a circle with 
center (h,k) and radius r.

You have to make your equation

x² + y² = 25

look like this:

(x - h)² + (y - k)² = r²

So
1. write the x as (x - 0)
2. Write the y as (y - 0)
3. Write the 25 as 5².

Then 

x² + y² = 25

becomes

(x - 0)² + (y - 0)² = 5²

So compare that to the standard
equation for a circle.

(x - h)² + (y - k)² = r²

and you can see that

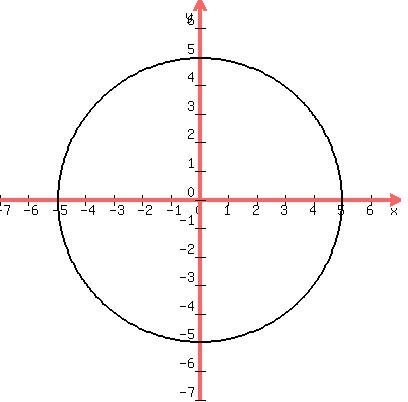
h = 0, k = 0, and r = 5.

So put the sharp point of a compass
at the center, which is (h,k) = (0,0),
or the origin, open the compass to 5
units, and draw the circle:


  
Edwin