SOLUTION: Please help me solve this question. A curve has the equation {{{y=acosbx+c}}} , with {{{a>0}}} . Given that the range of the curve is {{{-4>=y>=2}}} and that the period of t

Algebra ->  Average -> SOLUTION: Please help me solve this question. A curve has the equation {{{y=acosbx+c}}} , with {{{a>0}}} . Given that the range of the curve is {{{-4>=y>=2}}} and that the period of t      Log On


   

Question 1188590: Please help me solve this question.
A curve has the equation y=acosbx%2Bc , with a%3E0 . Given that the range of the curve is -4%3E=y%3E=2 and that the period of the curve is 180, evaluate a, b and c . Hence sketch the graph of y for 0%3C=x%3C=360 .
P.S. for before the 0, 180, and 360 there is a degrees sign it's just that I couldn't put it inside.
Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
the basic form of the graph of the cosine function is y = a * (b * (x - c)) + d.
a is the amplitude.
b is the frequency
c is the horizontal shift
d is the vertical shift.

the frequency is equal to 360 divided by the period.

if the period is 180, then the frequency is 360 / 180 = 2.

the equation becomes y = a * (2 * (x - c)) + d.

i think you mean -4 <= y <= 2.

the graph of y usually has the negative value of y below the positive value of y.
i haven't seen it the other way around.

since the range of y is from -4 to 2, then the total distance from the bottom of the cosine function to the top of the cosine function is 6.
the center line of the cosine function therefore has to be in the middle, i.e. 3 from the top and 3 from the bottom.
that puts the center line of the horizontal line equal to -1.
that makes d equal to 1.

the formula becomes y = a * (2 * (x - c)) - 1

it also makes the amplitude 6/3 = 3 because the amplitube is the distance from the horizontal center line of the graph.

the formula becomes y = 3 * (2 * (x - c)) - 1.

here does not appearw to be a horizontal shift, therefore c = 0 and is not shown.

the formula becomes y = 3 * (2 * x) + 1.

here's what the graph looks like.



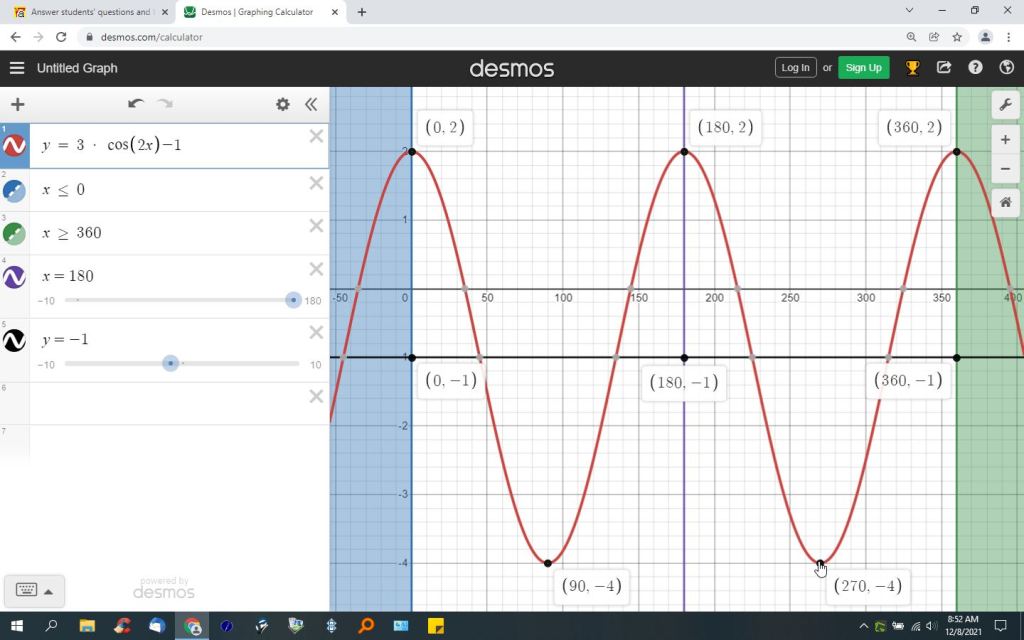
most of the reference use radians rather than degrees.

here's what the graph looks like in radians.



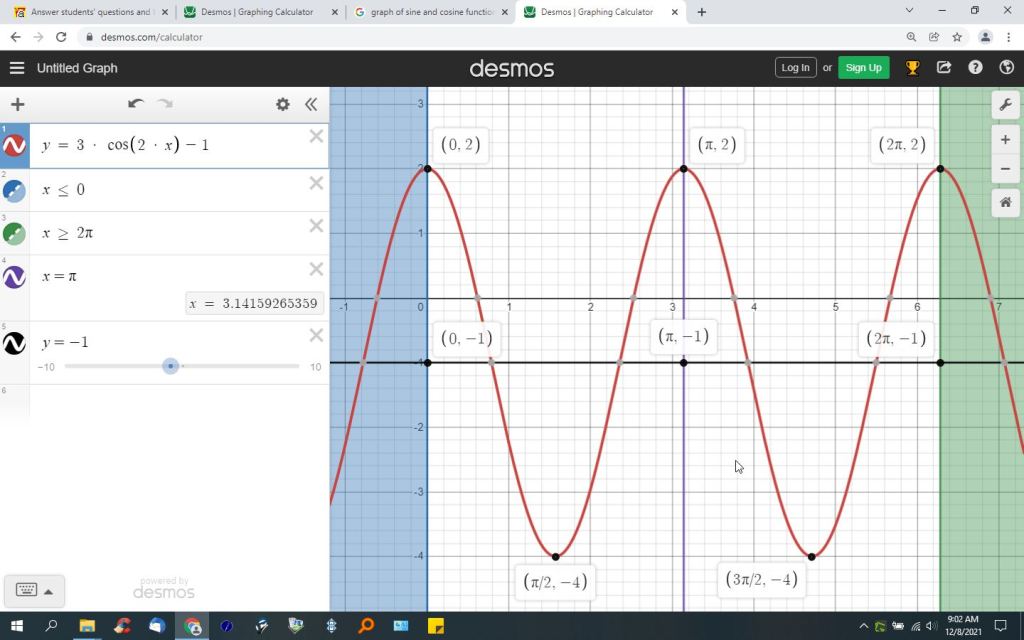
the formula to convert from radians to degrees is degrees = radians * 180 / pi.

the formula to convert from degrees to radians is radians = degrees * pi / 180.

here's a reference on graph of the sine and cosine functions.

https://mathbitsnotebook.com/Algebra2/TrigGraphs/TGsinusoidal.html

here's another one.

https://www.purplemath.com/modules/grphtrig.htm

let me know if you have any questions.

looking at what you had versus what i have, your c looks to be my d.
i could be wrong, but i didn't see any d in your version.

theo