Question 1188509: A ball is thrown vertically upward from the top of a building 64 feet tall with an initial velocity of 48 feet per second. The distances (in feet) of the ball from the ground
after t seconds is s(t) = 64 + 48t - 1612.
(a) After how many seconds does the ball strike the ground?
(b) After how many seconds will the ball pass the top of the building on its way down?
Found 2 solutions by ikleyn, Boreal:
Answer by ikleyn(52809)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A ball is thrown vertically upward from the top of a building 64 feet tall with an initial velocity of 48 feet per second.
The distances (in feet) of the ball from the ground
after t seconds is s(t) = 64 + 48t - 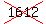 16t^2. 16t^2.
(a) After how many seconds does the ball strike the ground?
(b) After how many seconds will the ball pass the top of the building on its way down?
~~~~~~~~~~~~~~~~~~
Notice how I edited your post to make the formula correct.
(a) To answer question (a), solve this equation
-16t^2 + 48t + 64 = 0 (ground level)
First, simplify it by dividing both sides by -16
t^2 - 3t - 4 = 0.
To solve it, factor left side
(t-4)*(t+1) = 0.
Of two roots, t= 4 and t= -1, use only positive one t= 4 seconds. ANSWER
(b) To answer question (b), solve this equation
-16t^2 + 48t + 64 = 64 (top of the building level)
Simplify it
-16t^2 + 48t = 0
-16t(t - 3) = 0.
Of two roots, t= 0 and t= 3, only greater value t= 3 seconds is the solution to this part of the problem.
Solved and thoroughly explained.
///////////////
In this site, there is a bunch of lessons on a projectile thrown/shot/launched vertically up
- Introductory lesson on a projectile thrown-shot-launched vertically up
- Problem on a projectile moving vertically up and down
- Problem on an arrow shot vertically upward
- Problem on a ball thrown vertically up from the top of a tower
- Problem on a toy rocket launched vertically up from a tall platform
Consider these lessons as your textbook, handbook, tutorials and (free of charge) home teacher.
Read them attentively and learn how to solve this type of problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Projectiles launched/thrown and moving vertically up and dawn".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! The formula is s(t)=-16t^2+48t+64
the ground is 0.
so -16t^2+48t+64=0=t^2-3t-4, moving everything over and dividing by 16
(t-4)(t+1)=0
t=4 seconds.
-
want to know when s=64
so -16t^2+48t+64=64
or 16t^2=48t
t=3 seconds

|
|
|