SOLUTION: Find a formula for the quadratic function whose graph has y-intercept at y=15 and zeros at x=2 and x=4.

Since the zeroes are given x= 2 and x= 4, the parabola has the form


      y = a*(x-2)*(x-4).    (1)


The only thing we need is to determine the value of the unknown coefficient "a".


For it, write equation (1) at the given point (0,15), which is y-intercept.


So you substitute x= 0 into the formula (1) and equate it to 15


    15 = a*(-2)*(-4),

or

    15 = 8a,

which gives

    a = .


So the final expression for the quadratic function is  y = .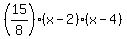


You may simplify it further, if you want or if you need.