Question 1188466: The radical 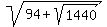 can be expressed as can be expressed as 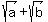 , where , where  . What is the product ab? . What is the product ab?
Found 2 solutions by ikleyn, mccravyedwin:
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
As posed, there is only one equation for finding two real numbers.
THEREFORE, the problem has INFINITELY many solutions ( more than billion ).
It is because the problem's posted formulation is INCORRECT.
Surely, I know the correct formulation and know the way to solve it,
but I do not want to make YOUR JOB, correcting your writing after you.
In accordance with the rules of this forum ( and in accordance
with the human common sense ), it is your duty
and your responsibility to provide a correct input.
/////////////
Edwin, when you start criticize me, you contradict to yourself.
From your post, you agree with me that 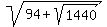 can be presented as can be presented as  by billion ways, by billion ways,
using different real numbers "a" and "b".
It immediately implies that the product a*b may have billion different values.
It was exactly what I said in my post.
Yes, if to add several other assumptions, like integer values for "a" and "b"
and some other mathematically indesribable assumptions like "simplicity of the terms",
then you will come to an expected answer, but these assumptions ARE NOT in the original formulation.
It was what I told in my post.
It is not me who "misinterpreted" this post.
It is you, who brought assumptions that there not in the original post.
What is strange to me (and it is why I write these lines), is to hear from you that I "misinterpreted" something in this problem.
In opposite, I interpreted it EXACTLY as it was written.
For your info, I solved TENS similar (but correctly formulated) problems in this forum,
and wrote several lessons related to these issues.
And I understand EXACTLY the hidden meaning of this problem: it is clear to me from the first glance.
I criticized the visitor and the creator of this post (for whom I think they both are the same person)
because they (or he) HIDE the true meaning of the problem.
Edwin, please do not explain me the meaning of such problems - it is clear to me from my 7-th grade class.
Do not spend your time for nothing.
Answer by mccravyedwin(407)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Ikleyn misinterpreted the problem. This is a common type problem of simplifying
expressions involving square roots occurring under square roots. While she is
right that there are an infinite number of values of a and b which would make
the equation
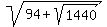   true, this is not what is asked for. What is being asked for is to find two
simple numbers, hopefully, positive integers, a and b, which will make the expression
true, this is not what is asked for. What is being asked for is to find two
simple numbers, hopefully, positive integers, a and b, which will make the expression
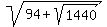 exactly equivalent to a simpler expression in the form
exactly equivalent to a simpler expression in the form
 ----------------------------------------------------------------------------
However, instead of doing your homework for you, I'll instead do one exactly
step-by-step like yours that you can follow as a model when solving yours. Here
is the problem I will do for you that is exactly like yours in every way:
----------------------------------------------------------------------------
However, instead of doing your homework for you, I'll instead do one exactly
step-by-step like yours that you can follow as a model when solving yours. Here
is the problem I will do for you that is exactly like yours in every way:
The radical 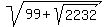 can be expressed as can be expressed as
 , where , where  . What is the product ab? . What is the product ab?
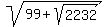   Square both sides:
equation (1):
Square both sides:
equation (1): 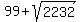  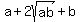 In equation (1), set the term WITHOUT a square root on the left equal to the sum
of the terms WITHOUT square roots on the right:
In equation (1), set the term WITHOUT a square root on the left equal to the sum
of the terms WITHOUT square roots on the right:
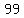  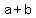 In equation (1), set the term WITH a square root on the left equal to the term
WITH a square root on the right:
In equation (1), set the term WITH a square root on the left equal to the term
WITH a square root on the right:
  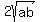 Square both sides:
Square both sides:
  
  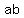 <---answer!
That's the answer you were asked for.
------------------------------------------------------
But in other problems, you WILL be asked to find a and b. So I will continue
to find the values of a and b:
Solve the system of equations: <---answer!
That's the answer you were asked for.
------------------------------------------------------
But in other problems, you WILL be asked to find a and b. So I will continue
to find the values of a and b:
Solve the system of equations:
 Solve the first equation for b:
Solve the first equation for b:
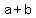  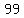
  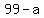 Substitute in the second equation in the system
Substitute in the second equation in the system
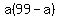  
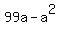  
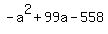  
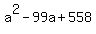  
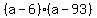   a-6 = 0; a-93 = 0
a = 6; a = 93
a-6 = 0; a-93 = 0
a = 6; a = 93
  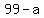 For a = 6 For a = 93
For a = 6 For a = 93
     
  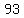    Since a < b, we choose a = 6 and b = 93
So the radical expression
Since a < b, we choose a = 6 and b = 93
So the radical expression 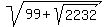 can be expressed as can be expressed as
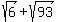 , where , where  Now do yours the exact same way, step-by-step.
Edwin
Now do yours the exact same way, step-by-step.
Edwin
|
|
|