SOLUTION: Given a right pyramid ABCDE, on a square base ABCD, with AB=8 cm, and height EO=5 cm, find the following: a) the angle EAB b)the angle β between a slant edge and the plane on

Algebra ->  Trigonometry-basics -> SOLUTION: Given a right pyramid ABCDE, on a square base ABCD, with AB=8 cm, and height EO=5 cm, find the following: a) the angle EAB b)the angle β between a slant edge and the plane on       Log On


   

Question 1187935: Given a right pyramid ABCDE, on a square base ABCD, with AB=8 cm, and height EO=5 cm, find the following:
a) the angle EAB
b)the angle β between a slant edge and the plane on the base
C) the angle θ between a slant face and the plane on the base.
Found 2 solutions by AnlytcPhil, Edwin McCravy:
Answer by AnlytcPhil(1810) About Me  (Show Source):
Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
  
The pyramid looks somewhat like this:



Let F be the midpoint of AB

Let's answer the last one first.
c) the angle θ between a slant face and the plane on the base.
△EOF is a right triangle
EO = 5

OF = (1/2)AB = (1/2)(8) = 4

θ = ∠OFE

tan(θ) = opp/hyp = EO/OF = 5/4
θ = 51.34019175 degrees  

------------------------------------------

We will need EF2 for the a) part, so

EF2 = EO2 + OF2 = 52 + 42 = 25 + 16 = 41
a) the angle EAB

△AFE is a right triangle
AF = (1/2)AB = (1/2)(8) = 4
AE2 = AF2 + EF2 = 42 + 41 = 16 + 41 = 57
∠EAB = ∠EAF 
cos(∠EAB) = cos(∠EAF) = adj/hyp = AF/AE = 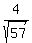4%2Fsqrt%2857%29
∠EAB = 58.007183 degrees

-----------------------------------
b)the angle β between a slant edge and the plane on the base

β = ∠OAE

OFA is a right triangle
AF = (1/2)AB = (1/2)(8) = 4
OF = (1/2)AB = (1/2)(8) = 4
AO2 = AF2 + OF2 = 42 + 42 = 16 + 16 = 32

AOE is a right triangle
tan(β) = tan(∠OAE) = opp/adj  = EO/AO = 5%2Fsqrt%2832%29 
β = 41.47293431 degrees

Edwin