SOLUTION: Events A and B are independent, P(A)=0.49 and P(A∪B)=0.83. Find P(A∩B) as a decimal or fraction.

Since Events A and B are independent, we can express  P(A∩B) as

    P(A∩B) = P(A)*P(B) = 0.49*P(B).      (1)



Next, we use the general formula for P(AUB)

    P(AUB) = P(A) + P(B) - P(A∩B).



We substitute here  P(AUB) = 0.83 (given);  P(A) = 0.49 (given)  and P(A∩B) = 0.49*P(B)  from (1).

We get then

    0.83 = 0.49 + P(B) - 0.49*P(B),


which gives

    0.83 - 0.49 = P(B)*(1-0.49),

        0.34    = 0.51*P(B)

        P(B) =  = .


Now from (1),  finally,   P(A∩B) = 0.49*P(B) = 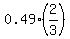 =  = 0.32666666...   ANSWER