Question 1187815: On one side of a path walk is a pedestal with a flag staff on top of it. The pedestal 2m in height while the flag staff is 3m high. At the opposite edge of the path walk the pedestal flag staff subtend
s equal angles. Compute the width of the path walk
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The way I read the problem, it looks like this:
 As seen across the walk path from an ant on the grass at the edge of the path opposite the pedestal, As seen across the walk path from an ant on the grass at the edge of the path opposite the pedestal,
the pedestal subtends an angle 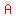 , and so does the flag staff. , and so does the flag staff.
With the path walk surface being horizontal, and the pedestal and flag staff being vertical,
I see two right triangles, sharing the path width as one leg.
The height of the pedestal, 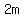 , is the other leg of one of those triangles, opposite angle , is the other leg of one of those triangles, opposite angle  . .
The sum of the heights of pedestal and flag staff,  , is a leg of the other triangle, opposite angle , is a leg of the other triangle, opposite angle  . .
If  path width in m, from those right triangles, we get the trigonometric ratios: path width in m, from those right triangles, we get the trigonometric ratios:
 and and 
Substituting those tangents into the trigonometric identity  , we get , we get
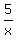  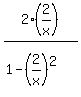 --> --> 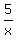  
Multiplying both sides times  , we get and equivalent equation: , we get and equivalent equation:
  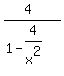
Assuming that  so that so that 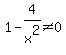 , we multiply both sides times , we multiply both sides times 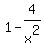 to get the equivalent equation to get the equivalent equation
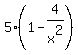   --> -->  --> -->  --> -->  --> -->  --> -->  --> --> 
The path is  wide. wide.
|
|
|