Question 1187758: a company tests its workers with a lie-detector that is correct 90% of the time and fires anyone fail the test suppose 5% of the workers are guilty of theft
1- for the workers who are fired ,calculate the percentage of them are actually guilty ?
Answer by ikleyn(52919)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a company tests its workers with a lie-detector that is correct 90% of the time and fires anyone
fail the test suppose 5% of the workers are guilty of theft.
1) for the workers who are fired, calculate the percentage of them are actually guilty ?
~~~~~~~~~~~~
The problem seems to be tangled, but it is because it is (intently ?) formulated in a way
to confuse the reader.
I will reformulate it, and then everything will become clear as at a sunny day.
a company tests its workers with a lie-detector. The device is correct in 90% cases,
which means that if it recognizes/detects lie/theft in 100 cases, then in 90 cases it is right.
Let the amount of people recognized as liers is 5% of the work force.
Among this 5% people, detected as liers, what is the percentage of those who are actually guilty ?
After my re-formulation, the ANSWER is as clear as 2 x 2 = 4:
90% of these 5% are actually guilty.
Or, in other words, 0.9*0.05 = 0.045 = 4.5% of total workers are actually guilty.
Solved, answered and explained.
/////////////
More advanced reader will notice that we are given the conditional probability
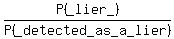 = 90% = 0.9 (*) = 90% = 0.9 (*)
and also are given that P(detected as a lier) = 0.05.
The question is to find P ( lier ).
Then from (*), we get the answer/answers formulated above.
|
|
|