|
Question 118770: Model each situation with a linear function and graph. Is it reasonable to include negative numbers in the range?
1.The weight of a bucket of golfballs is a function of the number of balls, each of which weighs 1.6 oz. The bucket itself weighs 2 lb.
2.It costs a farmer a $110 to bring 150 pounds of tomatoes to market, and the tomatoes sell for $2 per pound. The difference between the income from sales and the cost is the farmer's profit.
I'm sorry for asking so much. But my teacher told us to do our best, yet my best isnt good enough. Thanks sooo much! I Hope you answer soon!
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.The weight of a bucket of golfballs is a function of the number of balls, each of which weighs 1.6 oz. The bucket itself weighs 2 lb.
:
Let x = no. of golf balls
Let y = total weight of the golf balls including the bucket (in oz)
Since the balls are in oz, change the bucket weight to oz; 2 * 16 = 32
:
the total weight of the balls only, would be 1.6 * x, or just 1.6x
The equation including 1 bucket:
y = 1.6x + 32
:
Plot this equation from 0 to 25, it should look like this graph:

:
:
2.It costs a farmer a $110 to bring 150 pounds of tomatoes to market, and the tomatoes sell for $2 per pound. The difference between the income from sales and the cost is the farmer's profit.
:
Let x = no. of lbs of tomatoes up to 150 lb
Let y = profit
:
Income would be 2x
:
Subtract the cost of bringing them to market: 110
The profit if he sold 150 lb:
Profit = 2(150) - 110
Profit = 300 - 110
Profit = $190
:
The graph shows what happens when he sell less than 150 lb
:
Note that he has to sell: 2(55lb) = 110 to break even
Below 55 lb he will lose money, hence y is negative
:
y = 2x - 110
:
Plot this graph
:
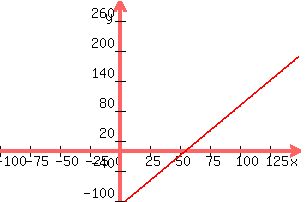
:
Negative values are useful in the tomato problem but not in the golf ball problem
:
Did you understand this and did it help you?
|
|
|
| |