This has us stumped.Its called Ms.DeYoungs BUNGEE
All numbers must meet the following requirements:
1. must be an even number
So it must have factor 2.
2. must be a multiple of 12
So it must contain the factor 12. That means that it
must have 2231 as a factor.
3.must be a perfect square
This means that it must have another 3 as a factor. So far
it must have 2232 as a factor.
4.must possess at least 1000 factors
We will use this number-of-factors rule (theorem):
If a positive integer is factored into its prime power factors,
then the total number of factors is found by adding one to all
the exponents and multiplying those results together.
So it must obey the above rule.
5.If written as a standard numeral, must have exactly four
terminal zeroes showing
This means it is a multiple of 10000. 10000 =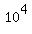 
=
2454. All the properties except property 4
are satisfied if 243254 is a factor.
A: 2 8th power X 3 4th power X 5 forth power X 17 4th power
This has 243254 as a factor so we
only need investigate to see if it meets the above
number-of-factors rule in property 4.
The exponents are 8,4,4,4. Add 1 to each one: 9,5,5,5. Multiply
9x5x5x5 = 1125. So it has 1125 factors. This is more than 1000,
So it meets all the properties.
B: 2 2nd power X 7 eigth power X 11 forth power X 17 sixth power
X 23 fifth power
243254 is not a factor of it so it does not have all the properties. It
needs to be multiplied by 223254 in order to have 243254 as a factor.
Its exponents are large enough for it to have 1000 factors,
so it does have property 4, since its exponents are 2,8,4,6,5;
adding 1 to each gives 3,9,5,7,6 and 3x9x5x7x6 = 5670.
C: 2 fourth power X 7 eigth power X 13 fourth power X 19 2nd power
243254 is not a factor of it
so it does not have all the properties. It needs to be multiplied
by 3254 in order to have 243254 as a factor. Its
exponents are not large enough for it to have 1000 factors, so it
does not have property 4, since its exponents are 4,8,4,2; adding
1 to each gives 5,9,5,3 and 5x9x5x3 = 675. If we multiplied it by
3254 then it would have at
least 1000 factors.
D: 2 fourth power X 3 eigth power X 5 fourth power X 13 2nd power X 97
This has 243254 as a factor so we only need investigate to see
if it meets the above number-of-factors rule in property 4.
The exponents are 4,8,4,2,1. Add 1 to each one: 5,9,5,3,2. Multiplying
5x9x5x3x2 = 1350. So it has 1350 factors. This is more than 1000,
So it meets all the properties.
E: 3 fifth power X 5 seventh power X 11 fourth power X 13 2nd power X 23
243254 is not a factor of it so it does not have all the properties.
It needs to be multiplied by 24 in order to have 243254 as a factor. Its exponents
are large enough for it to have 1000 factors, so it does have property 4,
since its exponents are 5,7,4,2,1; adding 1 to each gives 6,8,5,3,2 and
6x8x5x3x2 = 1440
F: 2 sixth power X 3 2nd power X 5 forth power X 7 forth power X 23
sixth power
This has 253254 as a factor so we only need
investigate to see if it meets the above number-of-factors rule in property 4.
The exponents are 6,2,4,4,6. Add 1 to each one: 7,3,5,5,7. Multiply
7x3x5x5x7 = 3675. So it has 3675 factors. This is more than 1000,
So it meets all the properties.
Edwin
