Question 1187610: Find the absolute extrema of the function on the closed interval.
f(x) = x^3 − 3/2x^2, [−3, 4]
maximum (x, y) =
Find the absolute extrema of the function on the closed interval.
y = 3x^2/3 − 2x, [−1, 1]
maximum (x, y) =
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the absolute extrema of the function on the closed interval.
  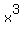 , [−3, 4] , [−3, 4]
The absolute extrema are either points at which the derivative is 0 or
undefined, or the endpoints of the interval, -3 or 4.
   which we set = 0 which we set = 0
  
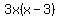  
 Points where derivative is 0 are (0,0) and (3,13.5)
Endpoints:
Points where derivative is 0 are (0,0) and (3,13.5)
Endpoints:
 So the absolute maximum point is (4,40)
and the absolute minimum point is (-3,-40.5).
So the absolute maximum point is (4,40)
and the absolute minimum point is (-3,-40.5).
Find the absolute extrema of the function on the closed interval.
y = 3x^2/3 − 2x, [−1, 1]
Do it the same way all by yourself. This time one of the absolute extrema
will be an an endpoint and the other at a point where the derivative is 0.
Edwin
|
|
|