|
Question 1187539: a man is paid 150 pesos for each day, he works and forfeits 50 pesos for each day he is idle. if at the end of 100 days he nets 10,000 pesos. how many days was he idle?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! he gets 150 pesos when he works.
he forfeits 50 pesos when he doesn't work.
let x = the number of days he works.
let y = the number of days he is idle.
at the end of 100 days, determine the number of days he was idle.
you have two equations that need to be solved simultaneously.
the first equation is x + y = 100
this equation is telling you how many days he worked (x) and how many days he was idle (y).
you don't know the value of x and y just yet, but will after solving the equations simultaneously.
the second equation is 150x - 50y = 10,000
this equations tells you the total amount of money he made when he worked (150 * x) and the total amount of money he lost when he was idle (-50 * y).
to solve them simultaneously, you need to eliminate one of the variable so you can solve for the other.
there are various ways to do this.
one way is shown below.
the two equations are:
x + y = 100
150x - 50y = 10,000
multiply both sides of the first equation by 50 and leave the second equation as is to get:
50x + 50y = 5,000
150x - 50y = 10,000
add both equations together to get:
200x = 15,000
solve for x to get:
x = 15,000 / 200 = 150 / 2 = 75.
since x + y = 100, then y must be equal to 25.
to confirm the value of x and y are good, replace x and y with them in the original equation to get:
x + y = 100 becomes 75 + 25 = 100 which becomes 100 = 100 which is correct.
150x - 50y = 10,000 becomes 150 * 75 - 50 * 25 = 10,000 which becomes 11,250 - 1250 which becomes 10,000 = 10,000 which is correct.
the values of x and y are good.
the above method was by elimination.
it's a good method to learn because it's used a lot in future problems you might encounter later on.
another method is by substitution.
that method works as shown below:
your two original equations are:
x + y = 100
150x - 50y = 10,000
solve for y in the first equation to get:
y = 100 - x
replace y with (100 - x) in the second equation to get:
150x - 50 * (100 - x) = 10,000
simplify to get:
150x - 5000 + 50x = 10,000
combine like terms to get:
200x - 5000 = 10,000
add 5000 to both sides of the equation to get:
200x = 15,000.
solve for x to get:
x = 15,00 / 200 = 75.
this makes y = 25 and you're good to go.
the third method is by graphing.
this method works ok with two variable equation, but is useful when the number of variable becomes greater than two.
it may also not give you as exact a solution as you want, depending on the software used, or by how accurate you can view the intersection point.
the graphing solution is shown below, using the desmos.com graphing software.
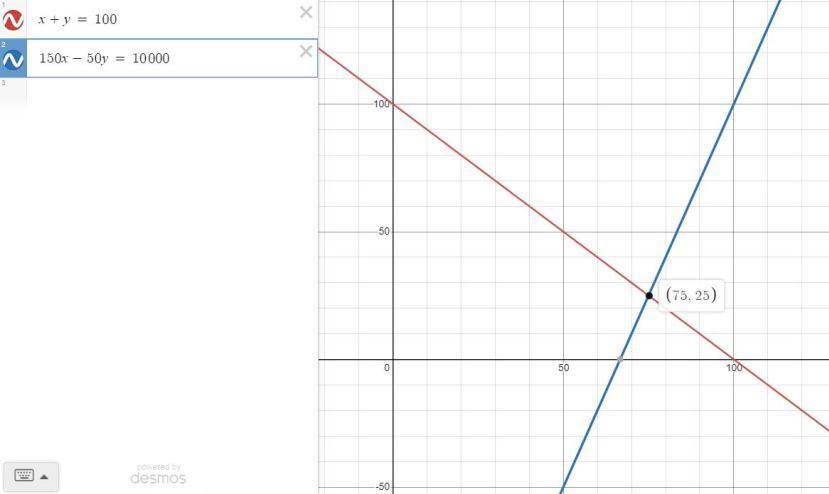
the intersection is at coordinate point (x,y) = (75,25).
that means x = 75 and y = 25.
here's a reference on solving equations simultaneously that is pretty good.
https://www.purplemath.com/modules/systlin1.htm
|
|
|
| |