|
Question 1187468: You are running a foundation for street children. Mr. Park, a rich benefactor, offers two options for his donations :
OPTION A: To give $ 1,000 on day 1, $999 on day 2, $998 on day 3, with the process to end after 1,000 days.
OPTION B: To give $1 on day 1, $2 on day 2, $4 on day 3, for 19 days.
You have to tell him today which option you want to take.
Answer by ikleyn(52884)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
You are running a foundation for street children. Mr. Park, a rich benefactor, offers two options for his donations :
OPTION A: To give $ 1,000 on day 1, $999 on day 2, $998 on day 3, with the process to end after 1,000 days.
OPTION B: To give $1 on day 1, $2 on day 2, $4 on day 3, for 19 days.
You have to tell him today which option you want to take.
~~~~~~~~~~~~~~~~~~~~~~
OPTION (A) : You need to find the sum of the first 1000 natural numbers
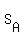 = 1000 + 999 + 998 + . . . + 2 + 1.
In your high school, you diligently learned about arithmetic progression, and you know
that the sum of the first n natural numbers is = 1000 + 999 + 998 + . . . + 2 + 1.
In your high school, you diligently learned about arithmetic progression, and you know
that the sum of the first n natural numbers is  .
So, you have a happy opportunity to apply your knowledge, and you quickly calculate .
So, you have a happy opportunity to apply your knowledge, and you quickly calculate
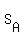 = = 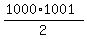 = 500*1001 = 500500 dollars.
OPTION (B) : You need to find the sum of the first 19 terms of the geometric progression
with the first term of 1 and the common ratio of 2. = 500*1001 = 500500 dollars.
OPTION (B) : You need to find the sum of the first 19 terms of the geometric progression
with the first term of 1 and the common ratio of 2.
 = =  + +  + + 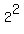 + . . . + . . .  .
In your high school, you diligently learned about geometric progression, and you know
that the sum of the first n terms of the given progression is .
In your high school, you diligently learned about geometric progression, and you know
that the sum of the first n terms of the given progression is  .
So, you have a happy opportunity to apply your knowledge, and you quickly calculate .
So, you have a happy opportunity to apply your knowledge, and you quickly calculate
 = = 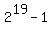 = 524287 dollars.
Now you have everything to make your decision and announce it to Mr. Park. = 524287 dollars.
Now you have everything to make your decision and announce it to Mr. Park.
I am sure you will make a right decision, and the street children will be happy ( ! )
----------------
Solved.
|
|
|
| |