Question 1187457: In the diagram below, Triangle ABC is isosceles, and Triangle MPQ is equilateral. Find the length, in cm, of Line PC.
Diagram:
https://ibb.co/2kGmVg2
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52776)   (Show Source): (Show Source):
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The link worked for me.
We know that triangle is a n isosceles right triangle, so angles A and C are
both 45°. Since we know that triangle ABC is an isosceles right triangle, we
can use ratio and proportion with the standard 45-45-90 right triangle to find
BC:
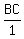  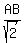
  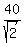 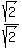
  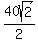  
 We need to prove that triangles ANQ and BNP are congruent. We cannot just
assume that they are. But all we have is SSA, which does not prove that two
triangles are congruent. However, the SSA theorem is an "either/or" theorem:
The SSA theorem can be stated this way:
If two sides and the non-included angle of one triangle are equal to the
corresponding sides and angle of another triangle, the two triangles are either
1. congruent
or
2. the other non-included angles are supplementary.
So we must rule out the possibility that angles AQN and BPN are supplementary.
AN = NB because they are both 20. Angle NAQ = angle NBP and NQ = NP because they
are sides of an equilateral triangle. So by the SSA theorem, either triangles
ANQ and BNP are congruent or angles AQN and BPN are supplementary.
Let's let angle QPC have measure a. Let's put in the values of the angles at P and Q:
We need to prove that triangles ANQ and BNP are congruent. We cannot just
assume that they are. But all we have is SSA, which does not prove that two
triangles are congruent. However, the SSA theorem is an "either/or" theorem:
The SSA theorem can be stated this way:
If two sides and the non-included angle of one triangle are equal to the
corresponding sides and angle of another triangle, the two triangles are either
1. congruent
or
2. the other non-included angles are supplementary.
So we must rule out the possibility that angles AQN and BPN are supplementary.
AN = NB because they are both 20. Angle NAQ = angle NBP and NQ = NP because they
are sides of an equilateral triangle. So by the SSA theorem, either triangles
ANQ and BNP are congruent or angles AQN and BPN are supplementary.
Let's let angle QPC have measure a. Let's put in the values of the angles at P and Q:
 So angles AQN and BPN are not supplementary, because (30+a)+(120-a) equals
150, not 180. Thus by the SSA theorem, triangles ANQ and BNP are congruent,
and 30°+a = 120°-a
2a = 90°
a = 45°
Next we will put in the actual numerical values for the angles at P and Q.
So angles AQN and BPN are not supplementary, because (30+a)+(120-a) equals
150, not 180. Thus by the SSA theorem, triangles ANQ and BNP are congruent,
and 30°+a = 120°-a
2a = 90°
a = 45°
Next we will put in the actual numerical values for the angles at P and Q.
 Now we can find BP for we have ASA in triangle BNP. We use the law of sines.
Now we can find BP for we have ASA in triangle BNP. We use the law of sines.
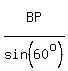  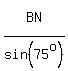
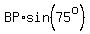  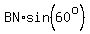
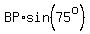  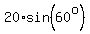 We know that
We know that 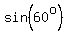   and and
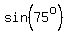  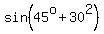  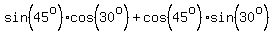 
  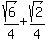  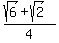 Substituting:
Substituting:
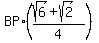  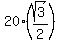
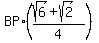  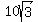 Multiplying both sides by 4:
Multiplying both sides by 4:
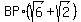  
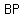  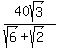 Rationalizing,
Rationalizing,
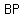  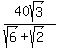  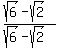  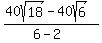  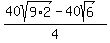 
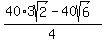  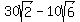 Now since PC = BC - BP and BC =
Now since PC = BC - BP and BC = 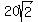  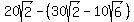
  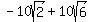
  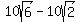
  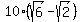 Edwin
Edwin
|
|
|