Question 1187450: You have a good credit score, $100,000 for a down payment, and $2,500 per month available for mortgage payments. The current fixed interest rate is 2.5% for a 5 year term and you are seeking an amortization period of 25 years involving monthly payments.
a) Identify the address and purchase price of the home that you can afford.
b) Identify the amount of principal paid after the first 5 year term.
c) Identify the amount of interest paid after the first 5 year term.
d) Determine the outstanding balance after 15 years.
e) Outline how your monthly payment would change if the interest rate rose to 4.5%
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you have 100,000 plus 2500 a month available to spend on a mortgage.
a very large assumption is that you have additional money available to spend on taxes and maintenance and other expenses such as food and transportation and whatever else you would need money for, since these have to be considered in a real world situation.
the first consideration is the price of the home you can buy.
the mortgage is assumed to be a 25 year mortgage at 2.5% per year compounded monthly.
use a financial calculator and input the following:
present value = 0
future value = 0
number of months = 25 * 12 = 300.
interest rate per month = 2.5% / 12 = .20833333333...% per month.
payment at the end of each month is equal to 2500.
solve for present value to get 557,268.56.
add 100,000 down payment to that to get value of the house equal to 657,268.56.
that's how much house you can buy with the money that you have available.
as long as you stay below 657,268.56, you can afford the house.
here's a house that costs 650,000 that you should be able to afford.
https://www.zillow.com/homedetails/50-Sylvan-St-Rutherford-NJ-07070/38024852_zpid/
the present value of the mortgage is 557,268.56.
650,000 minus that = 92,731.44.
that's how much you would put down.
you have 7,268.56 additional cash available that is the difference between 100,000 and 92,731.44.
after 5 years, which is 60 months, .....
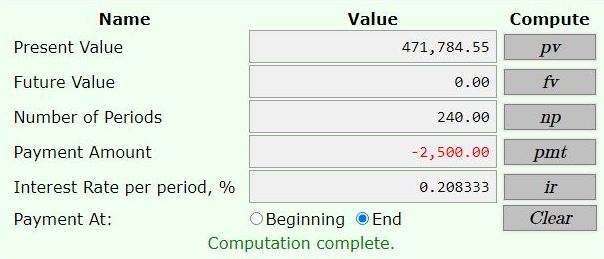
the remaining balance is $471,784.55.
the total payments made is 60 * 2500 = $150,000.
the equity paid is the original mortgage balance of $557,268.56 minus $471,784.56 = $85,484.
the interest paid is the sum of the payments minus the equity paid = 150,000 minus 85,484 = $64,516.
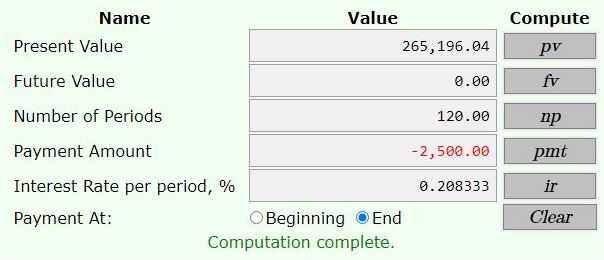
after 15 years, which is 180 months, the remaining balance is $265,195.99.
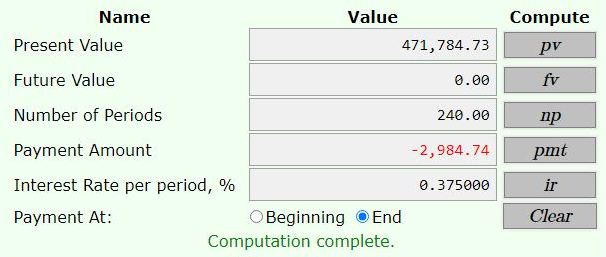
after the first 5 years, if the interest rate goes to 4.5% per year, then the payments would be increased to $2,984.74 for the remaining 20 years (= 240 months) of the loan.
here are the calculations used to get these figures.
the first one is used to find the present value for the 25 year loan at 2.5% interest rate per year compounded monthly.
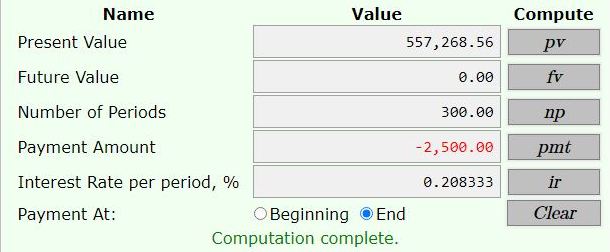
the second one is used to find the remaining balance after 5 years = 60 months.
you basically use the same payments and the same interest rate for 240 months which is the number of months remaining on the loan after 60 months (300 minus 60 = 240 months remaining on the loan).
the present value for that is the remaining balance of the loan after 60 months.
the sum of payments is 2500 * 60 = $150,000.
the remaining balance on the loan is $471,784.55.
the original balance on the loan was $557,268.56.
the equity portion of the payments was the difference = $85,484.
the interest charged was 150,000 minus 85,484 = 64,516.
the third one is used to find the remaining balance after 15 years = 180 months.
you basically use the same payments and the same interest rate for 120 months which is the number of months remaining on the loan after 15 years = 240 months (300 minus 240 = 120 months remaining on the loan).
the remaining balance is $265,195.99.
the fourth one takes the remaining balance on the loan after 60 months and raises the interest rate to 4.5% per year compounded monthly and then solves for the payment for the remaining 240 months of the loan.
the interest rate becomes 4.5/12 = .375% interest per month.
the payment becomes $2,984.74 per month, rounded to 2 decimal places.
let me know if you have any questions.
theo
|
|
|