Question 1187402: The questions are as follows:
On a shelf there are 4 different mathematics books and 8 different English books.
i) The books are to be arranged so that the mathematics books are together. In how many different ways can this be done?
Answer: 4!*9! = 8 709 120
I did not have any problem with the question and answer above, but the problem is the next one:
ii) What is the probability that none of the mathematics books are next to each other?
The working given for this question is ((8!)*(9P4))/(12!), but could anyone explain what is the logic behind this working?
Answer by ikleyn(52818)   (Show Source):
You can put this solution on YOUR website! .
So, I do not touch part (1) and am focusing on part (2), merely.
Imagine 8 different English books on the shelf.
Assume that they are not tightly placed each to other, having gaps between them.
We should place Math books into these gaps: one (and no more than one) Math book into each of 7 gaps.
Add to it one potential place on the left of 8 English books and one potential place on the right of 8 English books.
So, you have 7+1+1 = 9 potential places for 4 Math books.
It explains this factor 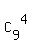 , which you see in the formula.
Also, 8 English books can be ordered in 8! ways.
It explains the factor 8! in the formula.
Now, the numerator 8!*C[9]^4 is the number of all favorable dispositions.
The denominator 12! = (8+4)! is the number of ALL potential placements of the books on the shelf.
The ratio of  to  ,  , is the probability, which you are seeking for.
Do you understand my explanation/explanations in full ?
|
|
|
