SOLUTION: Question 3.7/12 Let f(x)=(x+1)2 Give the largest domain on which f is one-to-one and non-decreasing= Give the range of f= Find the inverse of f restricted to the domain ab

Algebra ->  Functions -> SOLUTION: Question 3.7/12 Let f(x)=(x+1)2 Give the largest domain on which f is one-to-one and non-decreasing= Give the range of f= Find the inverse of f restricted to the domain ab      Log On


   

Question 1187396: Question 3.7/12
Let f(x)=(x+1)2
Give the largest domain on which f is one-to-one and non-decreasing=
Give the range of f=
Find the inverse of f restricted to the domain above f-1(x)=
Give the domain of f-1 =
Give the range of f-1=
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The function f%28x%29=%28x%2B1%29%5E2 is a quadratic function, meaning a polynomial function of degree 2.
Those functions have graphs like this graph%28110%2C100%2C2%2C7.5%2C1.5%2C6.5%2C%28x-5%29%5E2%2B2%29 or the same curve upside down.
They are symmetrical with a vertex that is a maximum or minimum, separating a decreasing branch from an increasing branch.
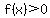You realize that for x=-1 , x%2B1=0 and f%28-1%29=0%5E2=0 , but for any other number f%28x%29%3E0 .
The graph decreases from any value of x%3C-1 , and increases for x%3E=-1 .
The largest domain on which f is one-to-one and non-decreasing is [-1,infinity), or x%3E=-1 .
The range is [0,infinity), because f%28-1%29=0, and for x%3E=-1 it increases without bounds.
To find the inverse we swap y and x in the function defined as y=%28x%2B1%29%5E2 only when x%3E=-1<-->x%2B1%3E=0 , and solve for y
we get x=%28y%2B1%29%5E2 for y%2B1%3E=0 , whose solution is sqrt%28x%29=y%2B1 <--> y=sqrt%28x%29-1 .
The inverse function is f%5E-1%28x%29=sqrt%28x%29-1 for X%3E=0 .
f%5E-1%28x%29=sqrt%28x%29-1 has domain [0,infinity) or x%3E=0 and range [-1,infinity) or y%3E=-1
The domain of an inverse function is the range of the domain-restricted function, and the range of the inverse is the restricted dominion.