Question 1187390: Assume that z is the test statistic.
(a) H0: 𝜇 = 22.5, Ha: 𝜇 > 22.5; x = 24.4, 𝜎 = 5.3, n = 25
(i) Calculate the test statistic z. (Round your answer to two decimal places.)
(ii) Calculate the p-value. (Round your answer to four decimal places.)
(b) H0: 𝜇 = 200, Ha: 𝜇 < 200; x = 194, 𝜎 = 39, n = 25
(i) Calculate the test statistic z. (Round your answer to two decimal places.)
(ii) Calculate the p-value. (Round your answer to four decimal places.)
(c) H0: 𝜇 = 12.4, Ha: 𝜇 ≠ 12.4; x = 11.4, 𝜎 = 4.1, n = 20
(i) Calculate the test statistic z. (Round your answer to two decimal places.)
(ii) Calculate the p-value. (Round your answer to four decimal places.)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! Assume that z is the test statistic.
in each of the following:
(i) Calculate the test statistic z. (Round your answer to two decimal places.)
(ii) Calculate the p-value. (Round your answer to four decimal places.)
the z-square formula, in this problem, would be:
z = (x - m) / se.
z is the z-score.
H0 is the null hypothesis
Ha is the alternate hypothesis
m is the assumed mean of the null hypothesis. this was probably based on previous studies. it could still be valid, or it could have changed.
x is the real mean of the alternative hypothesis as determined by the mean of the sample that was obtained.
se is the standard error of the mean.
se = sd / sqrt(ss)
se is the standard error of the mean.
sd is the standard deviation of the null hypothesis, in this case.
ss is the sample size.
the null hypothesis represents what the existing mean is assumed to be.
the alternative hypothesis represents what the test is trying to determine, i.e. whether the real mean is the same or different from the assumed mean, in some way, either not equal, greater, or less than the assumed mean.
(a) H0: 𝜇 = 22.5, Ha: 𝜇 > 22.5; x = 24.4, 𝜎 = 5.3, n = 25
se = 5.3 / sqrt(25) = 1.06
z = (x - m) / se = (24.4 - 22.5) / 1.06 = 1.79245283.
Ha equals greater than 22.5 which means they are testing to see if the real mean is greater than the assumed mean.
you are looking for the p-value of the area under the distribution curve that is to the right of the z-score.
the test p-value would be equal to .0365301771.
(b) H0: 𝜇 = 200, Ha: 𝜇 < 200; x = 194, 𝜎 = 39, n = 25
se = 39/sqrt(25) = 7.8
z = (x - m) / se = (194 - 200) / 7.8 = -.7692307692.
Ha equals less than 200 which means they are testing to see if the real mean is less than the assumed mean.
you are looking for the p-value of the area under the normal distribution curve that is to the left of the z-score.
the test p-value would be equal to .2208780931.
(c) H0: 𝜇 = 12.4, Ha: 𝜇 ≠ 12.4; x = 11.4, 𝜎 = 4.1, n = 20
se = 4.1 / sqrt(20) = .9167878708.
z = (x - m) / se = (11.4 - 12.4) / .9167878708 = -1.090764867.
Ha equals not equal to 12.4 which means they are testing to see if the real mean is not equal to the assumed mean.
it could be less than or it could be greater than.
in this particular case, the real mean is less than the assumed mean.
you are looking for the p-value of the area under the normal distribution curve that is to the left of the z-score.
the test p-value would be equal to .1376882174.
you can round these answer as you see fit.
the calsulator at https://www.calculatorsoup.com/calculators/statistics/z-score-calculator.php does it all for you.
it calculates the standard error from the standard deviation and the sample size and then calculates the z-score.
these are the results using that calculator.


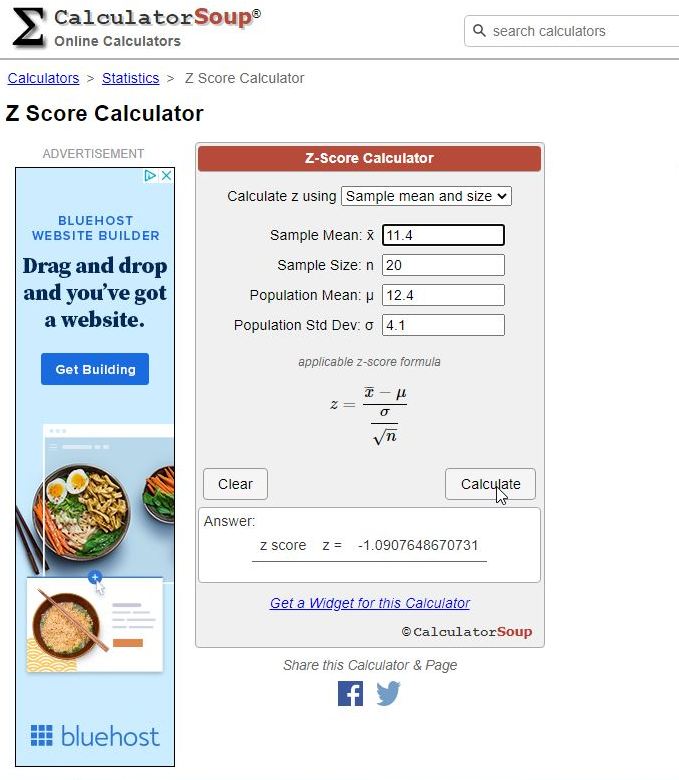
the calculator referenced above doesn't give you the p-value.
therre are other calculator that do that as well.
the calculator that i used is the ti-84 plus.
this is a physical calculator, not an online calculator.
other calculators get you the p-value, but they don't calculate the standard error for you.
they work off the z-score or they work off the raw score.
if they work off the z-score, the mean is 0 and the standard deviation is 1.
if they work off the raw score, the mean is the assumed mean from H0 and the standard deviation is the standard error that was derived from the sample size.
i haven't an online calculator yet that does it all for you.
even the ti-84 plus that i use assume you have calculated the standard error, if that's appropriate.
|
|
|