Question 1187261: Shortly after 5 o'clock, when the minute hand and the hour hand of the clock made a 90 degree angle, Ian went out to walk the dog. On his return, after 5:30, the two hands again made a 90 degree angle. For how many minutes was Ian out with his dog? (Tutor greenestamps has already answered this question, but I did not understand their solution. Does anyone mind explaining their solution more thoroughly or perhaps solving the question in a different way?) link to their solution: https://www.algebra.com/algebra/homework/word/mixtures/Mixture_Word_Problems.faq.question.1100328.html
Answer by ikleyn(52900)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Shortly after 5 o'clock, when the minute hand and the hour hand of the clock made a 90 degree angle,
Ian went out to walk the dog. On his return, after 5:30, the two hands again made a 90 degree angle.
For how many minutes was Ian out with his dog?
~~~~~~~~~~~~~~~~~~
We will measure angles starting from the position of the hour and the minute hands vertically up, at 12:00 (midday, the noon).
The minute hand makes one full rotation in one hour, so its angular velocity is 360 degrees per hour, or
360/60 = 6 degrees per minute.
The hour hand makes one full rotation in 12 hours, so its angular velocity is 360 degrees per 12 hours, or
360/12 = 30 degrees per hour = 30/60 = 0.5 degrees per minute.
At 5:00 pm, the hour hand is in position 5*30 = 150 degrees from vertical position clockwise.
The minute hand is in vertical position (= 0 degrees) at that time.
"t" minutes after 5:00 pm, the hour hand is in position 150 + 0.5t degrees from vertical up;
the minute hand is in position 6t degrees.
After 5:00 pm, the hour hand and the minute hand make the right angle for the first time, when 150 + 0.5t = 6t + 90 degrees.
From this equation, we find
150 - 90 = 6t - 0.5t, or 5.5t = 60, t = 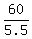 = 10.9090... minutes.
After 5:00 pm, the hour hand and the minute hand make the right angle for the second time, when 6t = 150 + 0.5.t + 90 degrees.
From this equation, we find
6t - 0.5t = 150 + 90, or 5.5t = 240, t = = 10.9090... minutes.
After 5:00 pm, the hour hand and the minute hand make the right angle for the second time, when 6t = 150 + 0.5.t + 90 degrees.
From this equation, we find
6t - 0.5t = 150 + 90, or 5.5t = 240, t = 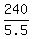 = 43.6363... minutes.
ANSWER. Ian was out with his dog 43.6363 - 10.9090 = 32.7272 minutes = 32 minutes and 44 seconds (rounded). = 43.6363... minutes.
ANSWER. Ian was out with his dog 43.6363 - 10.9090 = 32.7272 minutes = 32 minutes and 44 seconds (rounded).
Solved.
-------------------
On clock problems, see my lessons
- Clock problems
- Advanced clock problems
in this site.
|
|
|