Question 1187250: solve cos(3x) = cos(0.5x) for 0 <= x <= 180 degrees
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
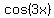  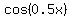 Write both angles in terms of their average.
Their average is
Write both angles in terms of their average.
Their average is 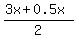  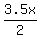  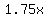
 and and  Substituting in original equation,
Substituting in original equation,
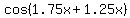  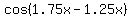
  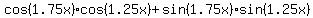
  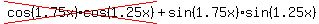
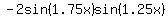  
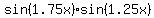  
   ; ; 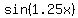  
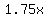   ; ; 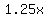   ; ;
 and and  so the above is so the above is
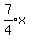   ; ; 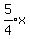  
  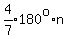 ; ;   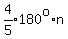
  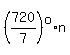 ; ;   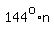 But since
But since  , ,
 , ,  , ,
 , ,  , ,
 , ,  , ,
 , ,  ,
Since n is an integer, n is either 0 or 1.
So the solutions are ,
Since n is an integer, n is either 0 or 1.
So the solutions are
  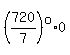 ; ;   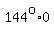 that is, x=0, and
that is, x=0, and
  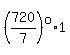 ; ;   
  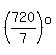 ; ;   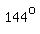 So there are 3 solutions.
So there are 3 solutions.
 , ,  , and , and  Edwin
Edwin
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I will get the same resulting answer, as Edwin, but will make my analysis differently.
To simplify my writing, I will introduce the angle y = 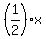 and
will look for angles y such that cos(6y) = cos(y) and 0 <= y <= 90 degrees.
Since cos(6y) = cos(y), it implies one of two possibilities:
(1) EITHER 6y = y + 360n degrees
(2) OR 6y = -y + 360n degrees.
From (1), I have 6y-y = 360n; 5y = 360n; y = 0, 360/5 = 72, (360/5)*2, . . .
Taking into account the restriction on the range, the only possible solutions are 0° and 72°.
From (2), I have 6y+y = 360n; 7y = 360n; y = 0, 360/7 = 51.43 degrees, (360/7)*2, . . .
Taking into account the restriction on the range, the only possible solutions are 0° and 360/7 degrees.
It gives the ANSWER : the only solutions for x are 0 degrees, 2*(360/5) = 144 degrees and 2*(360/7) degrees. and
will look for angles y such that cos(6y) = cos(y) and 0 <= y <= 90 degrees.
Since cos(6y) = cos(y), it implies one of two possibilities:
(1) EITHER 6y = y + 360n degrees
(2) OR 6y = -y + 360n degrees.
From (1), I have 6y-y = 360n; 5y = 360n; y = 0, 360/5 = 72, (360/5)*2, . . .
Taking into account the restriction on the range, the only possible solutions are 0° and 72°.
From (2), I have 6y+y = 360n; 7y = 360n; y = 0, 360/7 = 51.43 degrees, (360/7)*2, . . .
Taking into account the restriction on the range, the only possible solutions are 0° and 360/7 degrees.
It gives the ANSWER : the only solutions for x are 0 degrees, 2*(360/5) = 144 degrees and 2*(360/7) degrees.
Solved.
|
|
|