.
Packaging is one important feature in producing quality products. A box designer needs to produce a package
for a product in the shapes of the pyramid with a square base having a total volume of 200 cubic inches.
The height of the package must be 4 inches less than the length of the base. Find the dimension of the product
~~~~~~~~~~~~~~~~~~~
The "volume" equation is
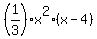 = 200 cubic inches,
or
= 200 cubic inches,
or
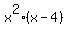 = 600.
One solution can be easily guessed: x = 10.
Indeed,
= 600.
One solution can be easily guessed: x = 10.
Indeed, 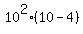 =
= 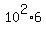 = 600.
Next, notice that the function
= 600.
Next, notice that the function 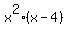 monotonically increases in its domain x > 4.
It means that x = 10 is the UNIQUE solution to the "volume" equation, and THERE IS NO other real solution.
ANSWER. Under given conditions, the unique set of the dimensions of the pyramid is 10 inches for the square base
and 6 inches for the height.
monotonically increases in its domain x > 4.
It means that x = 10 is the UNIQUE solution to the "volume" equation, and THERE IS NO other real solution.
ANSWER. Under given conditions, the unique set of the dimensions of the pyramid is 10 inches for the square base
and 6 inches for the height.
Solved.