Question 1187048: How many scalene triangles have perimeter less than 15 and sides of integral length?
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
scalene triangles have perimeter 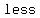 than than  and sides of integral length and sides of integral length
So with that understanding, there are  different triangles that meet the question’s criteria: different triangles that meet the question’s criteria:
[ , ,  , ,  ] ]
[ , ,  , ,  ] ]
[ , ,  , ,  ] ]
[ , ,  , ,  ] ]
[ , ,  , ,  ] ]
[ , ,  , , ] ]
[ , ,  , ,  ] ]
[ , , , , ] ]
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The response from the other tutor doesn't say anything about HOW to get the list of possible side lengths... and her list contains triangles with perimeters that are NOT less than 15.
The three side lengths are all different, because the triangle is scalene. Let a be the length of the shortest side, b be the length of the middle side, and c be the length of the longest side.
The length of the longest side must be less than the sum of the lengths of the other two sides.
Stated differently, the length of the shortest side has to be greater than the difference between the length of the longest side and the length of the middle side: a > c-b
(1) If a=1, then c-b has to be less than 1. But that makes b=c, and the triangle is not scalene. So there are no scalene triangles with integer side lengths with shortest side 1.
(2) If a=2, then c-b has to be less than 2; that means c has to be 1 more than b. The scalene triangles with integer side lengths, shortest side 2, and perimeter less than 15 are
(2,3,4)
(2,4,5)
(2,5,6)
(3) If a=3, then c-b has to be less than 3; so c has to be either 1 or 2 more than b. The scalene triangles with integer side lengths, shortest side 3, and perimeter less than 15 are
(3,4,5)
(3,4,6)
(3,5,6)
Similar analysis easily shows that there are no solutions to the problem with shortest side length greater than 3.
ANSWER: There are 6 different scalene triangles with integer side lengths and perimeter less than 15
|
|
|