Question 1186985: Hi
Mary bought some shoes and dresses for $296.00. The dress cost $24 the shoes $20 . How many of each did she buy.
Thanks
Found 2 solutions by josgarithmetic, greenestamps:
Answer by josgarithmetic(39630)   (Show Source):
You can put this solution on YOUR website! d, dresses
z, shoes
-
Look for combination of whole whole numbers which satisfy the equation.
---
Two possibilities
Shoes Dresses
4 9
10 4
Answer by greenestamps(13209)  (Show Source):
You can put this solution on YOUR website!
Here first is a refinement, using logical analysis and simple mental arithmetic, of the informal solution shown by the other tutor...
The total cost of all the items is $296, and the total cost of the shoes, at $20 per pair, is a multiple of $10.
That means the total cost of the dresses, at $24 each, must be a number with units digit 6.
That means the number of dresses must be 4, 9, 14, ...
Since 14 dresses at $24 each is more than $296, there are exactly two solutions -- with either 4 or 9 dresses.
And here is how to find the solution(s) using formal mathematics....
x = # of dresses at $24 each
y = # of (pairs of) shoes at $20 each
The total cost was $296:
Simplify...
Solve the equation for one variable
Perform the indicated division as quotient plus remainder, using integers -- instead of fractions
In that form of the equation, x and y are non-negative integers, and 14 is an integer, so 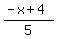 has to be an integer.
Inspection shows that x must be 4, or 4 plus or minus some multiple of 5.
Use that and the knowledge that x and y are both non-negative integers to find the solution(s).
(1) x=4
ANSWER: x=4 dresses and y=10 pairs of shoes
CHECK: 4($24)+10($20) = $96+$200 = $296
(2) x=9
ANSWER: x=9 dresses and y=4 pairs of shoes
CHECK: 9($24)+4($20) = $216+$80 = $296
(3) x=14
14($24) is greater than $296...
There are exactly two answers:
(1) 4 dresses and 10 pairs of shoes
(2) 9 dresses and 4 pairs of shoes
|
|
|
