SOLUTION: I was dealt a hand in bridge yesterday that had all 4 aces and 4 kings in the same hand. What are the odds of that happening?

I wish people wouldn't use the word "odds" when they mean "probability", which
is what was meant in all probability. lol.  If they are going to use "odds",
they should say "odds in favor" or "odds against", neither of which is the same
as probability.

A bridge hand consists of 13 cards. So there are 5 cards besides the 4 aces and
4 kings.  They are chosen from the other 52-8=44 cards, so there are
C(44,5)=1086008 ways that could happen.

The number of ways that any 13 cards could have been dealt is
C(52,13)=635013559600

So the probability of that happening is 1086008/635013559600 which reduces to
11/6431950, about 0.0000017

That means that on the average, you'll get such a hand only 11 times out of
every 6431950 times you are dealt a hand.  That's what "probability" means.

Now since you mentioned "odds", we must calculate how many times you will fail
to get such a hand. 

Since on the average, you'll get such a hand only 11 times out of every 6431950
times you are dealt a hand, then

on the average, you'll FAIL TO get such a hand a whopping 6431939 times out of every 
6431950 times you are dealt a hand. 

So your odds IN FAVOR OF getting such a hand is the ratio of 11 to 6431939, or
about 1 to 584721, often written with a colon 1:58471).
('Odds in favor' are usually given approximately as "1 in 'some number'".)

Your odds AGAINST getting such a hand is the ratio of 6431939 to 11, or about
584721 to 1, also often written with a colon 58471:1).
('Odds against' are usually given approximately as "'some number' to 1".)

So 



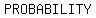
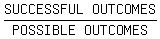and

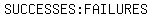 usually approximated by dividing both numbers by 
the number of SUCCESSES to make the first number in the ratio 1.

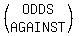
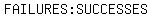 usually
approximated by dividing both numbers by the number of SUCCESSES to make the
second number in the ratio 1.

-----------------------------------------------------------------------

Now you know why I said what I said above about the word "odds". lol

ALSO, if you actually were dealt all 4 aces and all 4 kings, it is most likely
that the cards were not shuffled well after some card game that put them
together.

Edwin