SOLUTION: The function f is such that f(x) = 3x - 2 for x >= 0. The function g is such that g(x) = 2x^2 - 8 for x <= k, where k is a constant. (a) Find the greatest value of k for which

Algebra ->  Functions -> SOLUTION: The function f is such that f(x) = 3x - 2 for x >= 0. The function g is such that g(x) = 2x^2 - 8 for x <= k, where k is a constant. (a) Find the greatest value of k for which       Log On


   

Question 1186585: The function f is such that f(x) = 3x - 2 for x >= 0.
The function g is such that g(x) = 2x^2 - 8 for x <= k, where k is a constant.
(a) Find the greatest value of k for which the composite function fg can be formed.
(b) For the case where k = -3
(i) find the range of fg

(ii) find (fg)^-1(x) and state the domain and the range of (fg)^-1.
Answer by robertb(5830) About Me  (Show Source):
You can put this solution on YOUR website!
Given that the (restricted) domain of f(x) = 3x - 2 is [0,infinity), we need to choose the values of g%28x%29+=+2x%5E2+-+8+%3E=+0 for the composition f o g to be possible.

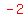(a) Hence, 2x%5E2+-+8+%3E=+0 ===> x%5E2+%3E=+4, or x ∈ (-infinity, -2] U [2, infinity). By virtue of continuity, the greatest value of k for which the composite function f o g can be formed is red%28-2%29.

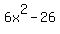(b) (i) Now %28f+o+g%29%28x%29+=+f%28g%28x%29%29+=+3%282x%5E2+-+8%29-2+=+6x%5E2++-26. Since the domain of f o g is (-infinity, -3], the expression 6x%5E2++-26 maps (-infinity, -3] onto the interval [28, infinity).
This is the range of (f o g)(x).

(ii) To find 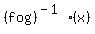%28f+o+g%29%5E%28-1%29%28x%29, let y+=++6x%5E2++-26.
===> x%5E2+=+%28y%2B26%29%2F6 ===> x+=+-sqrt%28%28y%2B26%29%2F6%29. (Choose the negative part since this is an element of (-infinity, -3].)
===> y+=+-sqrt%28%28x%2B26%29%2F6%29 after interchanging the places of x and y.

===> %28f+o+g%29%5E%28-1%29%28x%29+=+-sqrt%28%28x%2B26%29%2F6%29. Its domain is the range of f o g, namely [28, infinity), while its range is the domain of f o g, namely (-infinity, -3].