SOLUTION: A researcher believes that about 74% of the seeds planted with the aid of a new chemical fertilizer will germinate. He chooses a random sample of 90 seeds and plants them with the

The original problem is on Binomial distribution with n = 90 trials and  p = 74% = 0.74
for individual success.


So, formally there are standard formulas for binomial distribution, but the Math does not 
recommend to use it, because the formulas include high degree exponents and too great binomial
coefficients.  Instead, there is another, very effective and standard approach on solving such problems.


This approach is to use an appropriate normal distribution as an approximation to the Binomial distribution.


The relevant normal distribution has the mean  m = n*p = 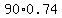 = 66.6
and the standard deviation  S = 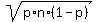 =  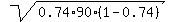= 4.16125.



This normal curve covers all 90 seeds on the horizontal axis, and we should take the area under
this normal curve on the right of the threshold value of 65.


A convenient tool for it is to use the standard function  normcdf (which means Cumulative Distrifution Function
for normal distribution).  This function is in any regular calculator like TI-83/84.


So, you write/print in your calculator

                 z1     z2    mean   SD     <<<---===  formatting pattern.
    P = normcdf(64.5,  9999,  66.6, 4.16125)


Here z1 = 64.5  stands for 65 and presents the continuing correction;  z2 stand for infinity on the horizontal axis,
mean is the mean and SD is the standard deviation.


Then the function will return the probability, which you are looking for: P = 0.6931.


It is the ANSWER to the problem's question  P = 0.6931, obtained with the normal distribution approximation.