|
Question 1186434: Derek’s shop sells shirts and pants. A pair of pants is sold at $48 and a shirt is sold
at 3/4 the price of a pair of pants. On Friday, Derek sold 2/3 of the clothing in his shop
and collected $3672. 2/5 of the clothing sold were pants.
(a) How many shirts did Derek sell on Friday?
(b) How many clothing were left unsold in the shop after Friday?
Found 3 solutions by ikleyn, Octo-pie7, MathTherapy:
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Derek’s shop sells shirts and pants. A pair of pants is sold at $48 and a shirt is sold
at 3/4 the price of a pair of pants. On Friday, Derek sold 2/3 of the clothing in his shop
and collected $3672. 2/5 of the clothing sold were pants.
(a) How many shirts did Derek sell on Friday?
(b) How many clothing were left unsold in the shop after Friday?
~~~~~~~~~~~~~~~~~~~~~
A pair of pants costs $48, and each shirt costs $36.
From the condition, we can say and write that Derec sold 2x pants and 3x shirts,
where an integer number x is the common factor.
With it, we can write the revenue equation as
48*(2x) + 36*(3x) = 3672.
Simplify and solve
96x + 108x = 3672
204x = 3672
x = 3672/204 = 18.
So, on Friday Derec sold 2x = 2*18 = 36 pants and 3x = 3*18 = 54 shirts.
The total clothing sold was 36+54 = 90 items.
These 90 item comprise 2/3 of the total clothing in his shop.
Nence, the number of unsold items in the shop was 90/2 = 45.
ANSWER. (a) On Friday, Derek sold 54 shirts.
(b) The number of unsold clothing was 45.
Solved.
Answer by Octo-pie7(11)   (Show Source): (Show Source):
You can put this solution on YOUR website! The price of one pair of pants is $48 and the shirt is sold at 3/4 the price of a pair of pants. Therefore the price of shirt is given by;
48 ⋅ 3/4 = 36
Therefore the price of a shirt is $36.
Now let x and y be the number of shirts and pants sold. On Friday 2/3 of the clothing in his shop are sold and he collected $3672. That is;
x ⋅ 36 + y ⋅ 48 = 3672 ⋯⋯⋯[÷12]
3x+4y=306
Now it is also given that 2/5 of the clothing sold were pants. So;
2/5(x + y)=y
2x + 2y = 5y
2x = 5y - 2y
2x = 3y
Applying this in the above equation;
3x + 4y = 306
3x + 4 2x/3 = 306 ⋯⋯⋯⋯[Therefore 2x=3y]
9x+8x/3 = 306
x = 306⋅3/17
= 54
Therefore 3y = 54 ⋅ 2
x = 54⋅2/3
= 36
Therefore 36 pants and 54 shirts were sold on friday.
It is given that Derek sold 2/3 of the clothing in his shop. For T being the total number of cloths in the shop;
2/3(T) = x+y
T = 3/2 (x + y)
= 135
Therefore cloths left on shop will be 1/3 of the cloths. So;
1/3 ⋅ 145 = 45
Therefore 45 cloths will be left unsold.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Derek’s shop sells shirts and pants. A pair of pants is sold at $48 and a shirt is sold
at 3/4 the price of a pair of pants. On Friday, Derek sold 2/3 of the clothing in his shop
and collected $3672. 2/5 of the clothing sold were pants.
(a) How many shirts did Derek sell on Friday?
(b) How many clothing were left unsold in the shop after Friday?
One of the other person's answers is WRONG! The number of shirts sold was NOT 36.
As  of clothing was sold, number of clothing sold = 2x, and number of unsold clothing = x
As of clothing was sold, number of clothing sold = 2x, and number of unsold clothing = x
As  of clothing sold were pants, number of pants sold = of clothing sold were pants, number of pants sold =  If
If  of clothing sold were pants, then of clothing sold were pants, then  of clothing sold, or of clothing sold, or  , were shirts
A pair of pants costs $48, and as a shirt cost ¾ a pants’ price, a shirt costs: ¾ * 48 = 36
Since , were shirts
A pair of pants costs $48, and as a shirt cost ¾ a pants’ price, a shirt costs: ¾ * 48 = 36
Since 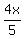 pants, and pants, and 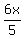 shirts sold for $3,672, we get: shirts sold for $3,672, we get:

 ------- Dividing by GCF, 12 ------- Dividing by GCF, 12
 16x + 18x = 5(306) ----- Multiplying by LCD, 5
34x = 5(306)
Number of unsold pieces of clothing, or
16x + 18x = 5(306) ----- Multiplying by LCD, 5
34x = 5(306)
Number of unsold pieces of clothing, or  Number of shirts sold:
Number of shirts sold: 
|
|
|
| |