.
f(x) = x^3 - 2 and g(x) = x^2 - 5x. Solve gf(x) = 6.
~~~~~~~~~~~~~
I am 179% sure that the problem in the post is written incorrectly.
The correct writing is THIS
f(x) = x^3 - 2 and g(x) = x^2 - 5x, solve gof(x) = 6. (1)
So, the left side of the equation is the composition of polynomials gof, and not their product gf.
After this correction, see my solution below.
Introduce new variable y = x^3 - 2.
Then the given equation (1) takes the form
y^2 - 5y = 6
or
y^2 - 5y - 6 = 0.
Factor left side
(y-6)*(y+1) = 0,
which gives the roots y= 6 and y= -1.
If y= 6, then x^3 - 2 = 6, x^3 = 6 + 2 = 8, which implies x = 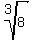 = 2.
If y= -1, then x^3 - 2 = -1, x^3 = -1 + 2 = 1, which implies x =
= 2.
If y= -1, then x^3 - 2 = -1, x^3 = -1 + 2 = 1, which implies x =  = 1.
So, the real roots of the equation (1) are the values 1 and/or 2.
If you want to get all complex roots of equation (1), you should obtain complex roots of equations
x^3 = 8 and x^3 = 1.
They are x =
= 1.
So, the real roots of the equation (1) are the values 1 and/or 2.
If you want to get all complex roots of equation (1), you should obtain complex roots of equations
x^3 = 8 and x^3 = 1.
They are x = 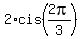 and
and  for equation x^3 = 8, and x =
for equation x^3 = 8, and x = 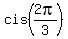 and
and  for equation x^3 = 1.
Thus the full list of the solutions to equation (1) is
1,
for equation x^3 = 1.
Thus the full list of the solutions to equation (1) is
1, 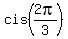 ,
,  , 2,
, 2, 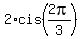 and
and  .
.
Solved.