SOLUTION: 1.) Write each fraction in terms of the LCM of the denominators. 15/16a3b3, 17/30a5b ??.. 2.) The Water Cube was built in Beijing, China, to house the National Swimming Center

Algebra ->  Equations -> SOLUTION: 1.) Write each fraction in terms of the LCM of the denominators. 15/16a3b3, 17/30a5b ??.. 2.) The Water Cube was built in Beijing, China, to house the National Swimming Center       Log On


   

Question 1186180: 1.) Write each fraction in terms of the LCM of the denominators.
15/16a3b3, 17/30a5b ??..
2.) The Water Cube was built in Beijing, China, to house the National Swimming Center for the 2008 Olympics. Although not actually a cube (its height is not equal to its length and width), the Water Cube is designed to look like a "cube" of water molecules. The volume of the 31-meter-high Water Cube is
971,199 m3.
Find the length of a side of its square base. Recall that
V = LWH. ??...
3.) A square piece of cardboard is formed into a box by cutting 10-centimeter squares from each of the four corners and then folding up the sides, as shown in the figure below. If the volume V of the box is to be 81,000 cm3, what size square piece of cardboard is needed? Recall that V = LWH. Length ??.. cm, Width ??.. cm. ??..

Answer by ankor@dixie-net.com(22740) About Me  (Show Source):
You can put this solution on YOUR website!
Write each fraction in terms of the LCM of the denominators.
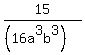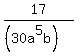
15%2F%28%2816a%5E3b%5E3%29%29, 17%2F%28%2830a%5E5b%29%29
LCM: 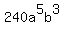240a%5E5b%5E3 so we have
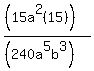%28%2815a%5E2%2815%29%29%29%2F%28%28240a%5E5b%5E3%29%29 = %28%28225a%5E2%29%29%2F%28%28240a%5E5b%5E3%29%29
and
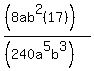%28%288ab%5E2%2817%29%29%29%2F%28%28240a%5E5b%5E3%29%29 = %28%28136b%5E2%29%29%2F%28%28240a%5E5b%5E3%29%29
:
:
2.) The Water Cube was built in Beijing, China, to house the National Swimming Center for the 2008 Olympics.
Although not actually a cube (its height is not equal to its length and width), the Water Cube is designed to look like a "cube" of water molecules.
The volume of the 31-meter-high Water Cube is 971,199 m3.
Find the length of a side of its square base.
Base is square and height 31,
therefore
31b^2 = 971199
b^2 = 971199/31
b = 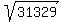sqrt%2831329%29
b = 177 meters
the dimensions: 177 by 177 by 31
:
:
3.) A square piece of cardboard is formed into a box by cutting 10-centimeter squares from each of the four corners and then folding up the sides, as shown in the figure below.
If the volume V of the box is to be 81,000 cm3, what size square piece of cardboard is needed?
:
let s = length and width of the cardboard,
Removing the 10 cm squares reduces the cardboard dimension by 20
The height is give as 10
(s-20)^2 * 10 = 81000
simplify, divide by 10, then square the sides
s^2 - 40s + 400 = 8100
s^2 - 40 + 400 - 8100 = 0
s^2 - 40s - 7700 = 0
Use the quadratic formula a=1, b=-40,c=-7700, but this will factor
(s-110)(s+70) = 0
positive solution
s = 110 cm the length of the square base
Dimensions of piece of cardboard; 110 by 110
Box dimensions: 90 by 90 by 10
Check
(110 - 20)^2 * 10 = 81000 cu/cm