SOLUTION: This a Abstract Algebra class Let G=⟨a⟩ be a cyclic group of order10. Define φ:Z→G by φ(n)=a^n for all n∈Z. Assume that φ is a homomorphism. Find kerφ.

Algebra ->  Test -> SOLUTION: This a Abstract Algebra class Let G=⟨a⟩ be a cyclic group of order10. Define φ:Z→G by φ(n)=a^n for all n∈Z. Assume that φ is a homomorphism. Find kerφ.      Log On


   

Question 1186053: This a Abstract Algebra class
Let G=⟨a⟩ be a cyclic group of order10. Define φ:Z→G by φ(n)=a^n for all n∈Z. Assume that φ is a homomorphism. Find kerφ.
Answer by ikleyn(52921) About Me  (Show Source):
You can put this solution on YOUR website!
.
This a Abstract Algebra class
Let G=⟨a⟩ be a cyclic group of order10. Define φ:Z→G by φ(n)=a^n for all n∈Z.
Assume that φ is a homomorphism. Find kerφ.
~~~~~~~~~~~~~~~` 

The group G is presented as  G = (a) in the post.

Also, from the context, G is a multiplicative group, regarding its operation.



It means that element "a" of the group G is the generator of the cyclic group G.



In turn, it means that 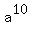 a%5E10 = 1  (the unit element of the group G),  

while  the elements 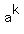 a%5Ek  at k = 1, 2, 3, . . . , 9 are all different and not equal to the unit element of the group.



Hence, kerφ is the set of all integers in Z that are multiples of 10:   { . . . , -20, -10, 0, 10, 20, . . . }.    ANSWER

Solved and explained.


===============


We should not  "assume"  that φ ,  defined in this way,  is a homomorphism.

It  REALLY  IS  the homomorphism.