|
Question 1186042: Some sweets were distributed equally among 24 children. Then 8 of
them gave away 2/3 of their sweets to the rest of the children. As a result,
each of the children receiving the additional sweets had 13 more sweets
than before. How many sweets were there in total?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52824)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Some sweets were distributed equally among 24 children. Then 8 of
them gave away 2/3 of their sweets to the rest of the children. As a result,
each of the children receiving the additional sweets had 13 more sweets
than before. How many sweets were there in total?
~~~~~~~~~~~~~~~
Let n be the total number of sweets (the unknown value under the problem's question).
Notice that the number of children giving away is 8;
the number of children receiving sweets is 24-8 = 16.
The number of sweets each child had at the beginning is 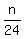 .
The number of sweets that 8 children gave to the rest of children was .
The number of sweets that 8 children gave to the rest of children was 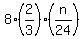 .
Now 16 children have, in total, .
Now 16 children have, in total,  + + 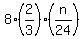 sweets.
The increment of sweets for each of 16 children is sweets.
The increment of sweets for each of 16 children is 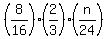 = =  .
This increment is equal to 13 .
This increment is equal to 13
 = 13.
Simplify and find n = 13.
Simplify and find n
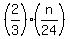 = 13*2 = 26;
n = = 13*2 = 26;
n = 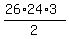 = 936.
ANSWER. The total sweets was 936. = 936.
ANSWER. The total sweets was 936.
Solved.
//////////////
Now, when the detailed analysis is completed and the problem is just solved,
you (and me) can see that other, more simple approach is possible.
The number of giving away children is 8;
the number of receiving is 16, two times as 8.
Each of 8 children gives away 2/3 of sweets.
Actually, every of 8 children gives (1/3) of what he (or she) has to two of 16 children.
Thus the increment for each of 16 is  of what everybody has at the beginning.
This one third is 13, according to the problem.
Hence, every child had 3*13 = 39 sweets at the beginning.
So the total sweets is 39*24 = 936. ! The same answer ! of what everybody has at the beginning.
This one third is 13, according to the problem.
Hence, every child had 3*13 = 39 sweets at the beginning.
So the total sweets is 39*24 = 936. ! The same answer !
Happy learning (!)
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The other tutor's second solution, presented a bit differently....
8 of the 24 children each gave 2/3 of their sweets to the other 16 children.
Since the number of children receiving sweets was twice the number of children giving away sweets, each of the 16 children receiving sweets received 1/3 of the number of sweets each child started with.
The number of sweets each of the 16 children received was 13; since that was 1/3 of what each child started with, the number of sweets each child started with was 3*13 = 39.
So the total number of sweets was 24*39 = 936.
ANSWER: 936
|
|
|
| |