Question 118579This question is from textbook McDougal Littel Algebra 2
: Find the number of possible 5-card hands that contain the card specified from a standard deck of 52 cards. get 5 face cards
This question is from textbook McDougal Littel Algebra 2
Found 2 solutions by checkley71, solver91311:
Answer by checkley71(8403)   (Show Source): (Show Source):
You can put this solution on YOUR website! GIVEN THAT YOUR DEFINITION OF FACE CARDS ARE:10,J,Q,&K.
THEN WE HAVE A 5 CARD HAND OF 16*15*14*13*12=514,160 POSSIBLE DIFFERENT HANDS.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are 3 face cards, K, Q, and J, in each of the four suits, so there are a total of 12 face cards in the deck. The probability that the first card dealt will be a face card is 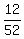 because there are only 12 successful outcomes out of 52 total possible outcomes. because there are only 12 successful outcomes out of 52 total possible outcomes.
Once the first card has been selected, and we have the partial successful outcome of drawing a face card (the complete successful outcome being a five card hand consisting of only face cards), we are left with a deck that contains 51 cards, 11 of which are face cards. That means the probability of drawing a second face card is  . .
Likewise, the probability for the 3rd, 4th, and 5th cards being face cards is:
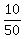 , ,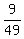 , and , and 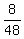 . .
Now the probability of all 5 cards being face is  or roughly 0.03 percent. In other words, 99.97 percent of the time it won't happen. or roughly 0.03 percent. In other words, 99.97 percent of the time it won't happen.
Super-Double-Plus Extra Credit What is the probability that you would be dealt 2 Kings and 3 other non-face cards?
|
|
|