Question 1185771: The acute angles of a right triangle have degree measures 30 and 60. If the side opposite the 60-degree angle has length 18, then what is the length of the side opposite the 30-degree angle?
Found 4 solutions by josgarithmetic, ikleyn, Edwin McCravy, mccravyedwin:
Answer by josgarithmetic(39630)   (Show Source):
You can put this solution on YOUR website! Draw the triangle; it is half of an equilateral triangle.
if x is the side opposite the 30 degree angle, 2x is the side opposite the right angle;
and you know what to do.
Answer by ikleyn(52879)  (Show Source):
You can put this solution on YOUR website! .
The acute angles of a right triangle have degree measures 30 and 60.
If the side opposite the 60-degree angle has length 18, then what is the length
of the side opposite the 30-degree angle?
~~~~~~~~~~~~~~~~~
The setup equation, which @josgarithmetic proposes you to solve in his post, IS INCORRECT,
and you will obtain NOTHING except incorrect answer and bad score, if will follow him.
I came to bring a correct solution to you.
Let x be the length of the side of the triangle opposite to 30-degrees angle.
Then the hypotenuse is 2x
The Pythagorean equation takes the form
x^2 + 18^2 = (2x)^2
x^2 + 18^2 = 4x^2
18^2 = 4x^2 - x^2
18^2 = 3x^2
x^2 = 18^2/3 = 324/3 = 108
x =  =  . ANSWER
Solved.
It is the long way to solve the problem. This way assumes that you are very beginner student,
not familiar well with the properties of the (30-60-90-degree) triangles.
More experienced students just know that the long leg of such triangle is  times as long as the shortest leg,
so they write  = 18, and from this equation quickly obtain
x =  =  = ,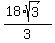
getting the same answer, as I developed for you in the first part of my post.
Solved (in two ways, for your better understanding).
---------------
For your safety, IGNORE the post by @josgarithmetic.
///////////////
After my notice, he changed his setup equation, simply re-wrote it from mine.
Answer by Edwin McCravy(20064)  (Show Source):
Answer by mccravyedwin(409)  (Show Source):
|
|
|
