SOLUTION: cos(5x)cos(3x)-sin(5x)sin(3x)=sqrt(3)/2, giving the exact solutions which lie in [0,2pi)

Algebra ->  Trigonometry-basics -> SOLUTION: cos(5x)cos(3x)-sin(5x)sin(3x)=sqrt(3)/2, giving the exact solutions which lie in [0,2pi)      Log On


   

Question 1185683: cos(5x)cos(3x)-sin(5x)sin(3x)=sqrt(3)/2, giving the exact solutions which lie in [0,2pi)
Answer by ikleyn(52810) About Me  (Show Source):
You can put this solution on YOUR website!
.

According to the addition formula for cosine arguments, the left side is  cos(5x+3x) = cos(8x).


Therefore, the given equation is EQUIVALENT to


    cos(8x) = sqrt%283%29%2F2


and has the solutions for 8x


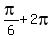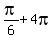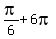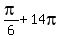    8x = pi%2F6,  pi%2F6+%2B+2pi,  pi%2F6+%2B+4pi,  pi%2F6+%2B+6pi, . . . , pi%2F6+%2B+14pi  (8 values)

or

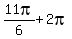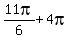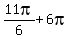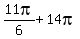    8x = 11pi%2F6,  11pi%2F6+%2B+2pi,  11pi%2F6+%2B+4pi,  11pi%2F6+%2B+6pi, . . . , 11pi%2F6+%2B+14pi  (another 8 values).


Dividing by 8, we get these 8 different solutions for x


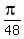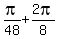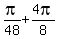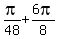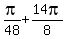    x = pi%2F48,  pi%2F48+%2B+2pi%2F8,  pi%2F48+%2B+4pi%2F8,  pi%2F48+%2B+6pi%2F8, . . . , pi%2F48+%2B+14pi%2F8  (8 values)

or

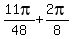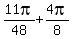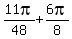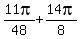    x = 11pi%2F48,  11pi%2F48+%2B+2pi%2F8,  11pi%2F48+%2B+4pi%2F8,  11pi%2F48+%2B+6pi%2F8, . . . , 11pi%2F48+%2B+14pi%2F8  (another 8 values).


The listed 8 + 8 = 16 values for x represent the full set of solutions to given equation in the interval [0,2pi).


You can make obvios reducing of fractions. I left the fraction in this form in order for you can better see the structure of the solution.

Solved, explained and completed.