Question 1185633: Find all values of x for which the graph of f lies above the graph of g. (Enter your answer using interval notation.)
f(x) = (1)/(x) g(x) = (1)/(x-7)
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!



Add the two fractions with a common denominator
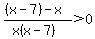

The denominator, and therefore the whole expression, changes sign at x=0 and x=7.
(-infinity,0): both factors in the denominator are negative, so the denominator is positive, so the expression is negative. The inequality is not satisfied.
(0,7): one of the factors in the denominator is negative, so the denominator is negative, so the expression is positive. The inequality is satisfied.
(7, infinity): both factors in the denominator are positive, so the denominator is positive, so the expression is negative. The inequality is not satisfied.
ANSWER: The graph of f(x) (red) lies above the graph of g(x) (green) on the interval (0,7)

|
|
|