SOLUTION: Use the inverse of the coefficient matrix to solve the system of equations. x+4y+3z=-40 x-6y-4z=65 2x+5y+4z=-32 Identify the inverse of the coefficient matrix.

 
Write your system with all three letters and their
coefficients showing (even when the coefficient is 0, 1
or -1):

 

When we write that system as a matrix equation we have:



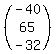where A = 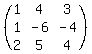, X = 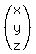, and B =  

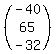Now you have to calculate the inverse of matrix A, which is called
the "coefficient matrix" because it consists of all the coefficients
of the three letters:

A =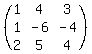 
 
Do you know how to find the inverse of a matrix?  If not post again
and we'll show you how.  I will just assume you can find that the inverse
is this matrix.  I'll color it red.  It is:

      <--That's the inverse of the coefficient matrix

Next we left multiply both sides of this matrix equation:



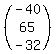by that red inverse matrix



and get this equation:



Now I will assume that you know how to multiply two matrices.  If
you don't know how, then post again asking how to.  When you
multiply the red matrices by the black matrices just to the right of
each red one, you get this:



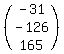Notice that when you multiply the inverse of a matrix by the matrix
of which it is the inverse you get the identity matrix, which has
1's on the diagonal and 0's elsewhere.

Now if you multiply the two matrices on the left, you get:



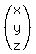
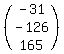and so x=-31, y=-126, and z=165.

Edwin