Question 118563: CAN YOU HELP ME. I REALLY DONT UNDERSTAND. I HAVE TO VERIFY THE GIVEN FACTORS OF THE FUNCTION, FIND THE REMAINING FACTORS OF f, USE MY RESULTS TO WRITE THE COMPLETE FACTORIZATION OF f, LIST ALL REAL 0'S OF f, AND CONFRIM MY RESULTS BY USING A GRAPHING ULTILITY TO GRAPH THE FUNCTION.
f(x)=2x(to the 3rd power)+x(to the 2nd power)-5x+2 Factors
(x+2) (x-1)
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! You need to use long division or synthetic division to verify that the given factors are indeed factors of the function. I'll try to walk you through the steps for one of them:

The first term of the denominator, x, goes into the first term of the numerator, 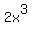 , ,  times, so that becomes the first term of your quotient. times, so that becomes the first term of your quotient.  so subtract these two terms from the first two terms of the numerator expression yielding so subtract these two terms from the first two terms of the numerator expression yielding 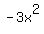 . Bring down the next numerator term and divide the resulting binomial, . Bring down the next numerator term and divide the resulting binomial,  , by , by  . The first term of the divisor, x, goes into the first term . The first term of the divisor, x, goes into the first term 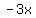 times, so that becomes the second term of your quotient. times, so that becomes the second term of your quotient.  . Subtract these two terms from the ( . Subtract these two terms from the ( dividend part resulting in dividend part resulting in  . Bring down the . Bring down the  resulting in resulting in  . Divide the . Divide the  by by  resulting in 1, which becomes the third term of your quotient. The quotient is now resulting in 1, which becomes the third term of your quotient. The quotient is now  and there is no remainder. Since there is no remainder, you have verified that and there is no remainder. Since there is no remainder, you have verified that  is a factor of is a factor of 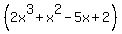 . .
Repeat the process using the quotient you just derived,  , and dividing that by the other given factor, , and dividing that by the other given factor,  . Since the process is the same as described above, I'll leave the details to you, but you should get a quotient of . Since the process is the same as described above, I'll leave the details to you, but you should get a quotient of  with no remainder. That tells you that with no remainder. That tells you that  is a factor and that the third factor is is a factor and that the third factor is  . .
Now you can say that  . The zeros of f are those values of x for which . The zeros of f are those values of x for which  . .
 if and only if if and only if  or or  or or  . .
Solving each of these equations yields:




Notice that the graph crosses the x-axis at the three zeros of f.
Notice that this graph has a peak and a valley. It's beyond the scope of this discussion why, but the values of x at the top of the peak and the bottom of the valley are given by solving  , yielding , yielding 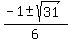 , very roughly speaking -1 and 3/4, as you can see on the graph. The y values for these points would obviously be the original function evaluated at these two x values. , very roughly speaking -1 and 3/4, as you can see on the graph. The y values for these points would obviously be the original function evaluated at these two x values.
Hope that helps.
John
|
|
|