|
Question 1185585: A ball is thrown directly upward from a height of 4 ft with an initial velocity of 24 ft/sec. The function s(t) gives the height of the ball, in feet, t seconds after it has been thrown. Determine the time at which the ball reaches its maximum height and find the maximum height.
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A ball is thrown directly upward from a height of 4 ft with an initial velocity of 24 ft/sec.
The function s(t) gives the height of the ball, in feet, t seconds after it has been thrown.
Determine the time at which the ball reaches its maximum height and find the maximum height.
~~~~~~~~~~~~~~~~~~
The function s(t) is s(t) = -16t^2 + 24t + 4.
The maximum height is reached when the quadratic function s(t) reaches its maximum.
It happens when t = " -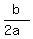 ", referring to the general form of a quadratic equation.
In your case a = -16, b = 24, THEREFORE, ", referring to the general form of a quadratic equation.
In your case a = -16, b = 24, THEREFORE, 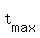 = = 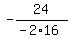 = = 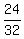 = =  of a second = 0.75 seconds.
The maximum height then is the height at t = of a second = 0.75 seconds.
The maximum height then is the height at t = 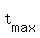 = 0.75 seconds = 0.75 seconds
 = -16*0.75^2 + 24*0.75 + 4 = 13 ft.
ANSWER. = -16*0.75^2 + 24*0.75 + 4 = 13 ft.
ANSWER. 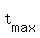 = 0.75 seconds; = 0.75 seconds;  = 13 ft. = 13 ft.
Solved.
----------------------
To see many other solved similar and different problems, see the lessons
- Introductory lesson on a projectile thrown-shot-launched vertically up
- Problem on a projectile moving vertically up and down
- Problem on an arrow shot vertically upward
- Problem on a ball thrown vertically up from the top of a tower
- Problem on a toy rocket launched vertically up from a tall platform
Consider these lessons as your textbook, handbook, tutorials and (free of charge) home teacher.
Read them attentively and learn how to solve this type of problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Projectiles launched/thrown and moving vertically up and dawn".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|
| |