Question 1185559: Q: Let the vertices of triangle be (0, 0), (3, 0) and (0, 4). Find its:
(i) Orthocenter (ii) Radius of the inscribed circle
Answer by ikleyn(52794)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Q: Let the vertices of triangle be (0, 0), (3, 0) and (0, 4). Find its:
(i) Orthocenter (ii) Radius of the inscribed circle
~~~~~~~~~~~~~~~~
You can make a sketch, or, like me, simply look attentively at coordinates of the vertices.
Then you will notice that the triangle is a RIGHT-ANGLED triangle with the right angle vertex
at the origin of the coordinate system.
THEREFORE, the othocenter (the intersection point of altitudes) is the origin point (0,0).
Next, in a right angled triangle, the radius of incribed circle is
r = 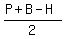 ,
where P and B are the legs and H is the hypotenuse.
In your case, P = 3, B = 4, H = 5, THEREFORE, the radius of the inscribed circle is
r = ,
where P and B are the legs and H is the hypotenuse.
In your case, P = 3, B = 4, H = 5, THEREFORE, the radius of the inscribed circle is
r = 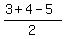 = = 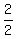 = 1 unit. = 1 unit.
Solved, answered, explained and completed.
|
|
|