Question 1185499: A factory is to be built on a lot measuring 270 ft by 360 ft. A local building code specifies that a lawn of uniform width and equal in area to the factory must surround the factory.
What must the width of the lawn be? ?
If the dimensions of the factory are A ft by B ft with A
and B= ?
Found 4 solutions by josgarithmetic, ikleyn, greenestamps, MathTherapy:
Answer by josgarithmetic(39615)   (Show Source):
Answer by ikleyn(52764)  (Show Source):
You can put this solution on YOUR website! .
A factory is to be built on a lot measuring 270 ft by 360 ft. A local building code specifies that
a lawn of uniform width and equal in area to the factory must surround the factory.
What must the width of the lawn be? ?
If the dimensions of the factory are A ft by B ft with A
and B= ?
~~~~~~~~~~~~~~~~~~~~~~
The answer for the uniform width 180 ft, which @josgarithmetic derived in his post,
is INCORRECT and TOTALLY ABSURDIST, since it does nor leave a room for the factory inside this lot.
I came to bring a correct solution and correct answer.
The outer dimensions of the lot are 270 ft by 300 ft.
The area of the lot is 270 x 360 = 97200 square feet.
The area of the factory must be half of it, i.e. 48600 square feet.
If u is the uniform width of the lawn, then the equation for the factory area is
(270-2u)*(360-2u) = 48600.
Simplify and reduce to the standard quadratic equation form
4u^2 - 2*270u - 2*360u + 97200 = 48600
4u^2 - 1260u + 48600 = 0
u^2 - 315u + 12150 = 0
Use the quadratic formula
 =  =  .
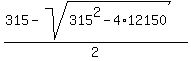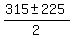Now, even by disarmed eyes, it is clear that  =  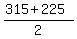= 270 is inappropriate solution,
since it is tooooo big, not leaving space/room for the factory.
The only remaining solution is  =  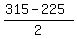=  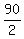= 45 feet.
Thus the uniform width is 45 feet, and the dimensions of the factory should be
270 - 2*45 = 180 feet and 360 - 2*45 = 270 feet. ANSWER
CHECK. The factory area 180*270 square feet is EXCATLY HALF of the lot area 360*270 square feet. ! Correct !
Solved.
/////////////
Now @josgarithmetic will be feverishly re-write his post, redoing calculations, to get into my numbers.
I observe his activity at this forum during many years.
Yet 3-4 years ago, his scores (the percentage of correctly solved problems) were 40 - 50%,
and I wrote about it in the forum, calling him "pseudo"-tutor.
Now his scores are about 10%, and it is just another category.
I know it very well, because I fixed wrong solutions after him every day several times per day.
The conclusion is: you, the visitor, should not trust NO ONE problem, solved, answered and presented by him.
\\\\\\\\\\\\\\\
Everything happened with his post as I predicted . . .
Answer by greenestamps(13196)  (Show Source):
You can put this solution on YOUR website!
There is no need to work with quadratic equations with big "ugly" numbers to solve this problem, if you first take a moment to do some logical reasoning and simple mental arithmetic.
The lot is 270 feet by 360 feet; the lawn surrounding the building is to be of uniform width; and the area of the building is to be half the area of the lot.
Observe that the difference between the length and width of the lot is 90 feet; with the lawn of uniform width, the difference between the length and width of the building must also be 90 feet.
So we need the dimensions of the building to be two numbers that differ by 90 and whose product is half of 270*360.
Now if we look at that requirement before plunging into some algebra with big numbers, we can see that half of 270*360 is 270*180 -- and those dimensions satisfy the requirement that they differ by 90.
So the building is 180 feet by 270 feet. Each dimension of the building is 90 feet less than the corresponding dimension of the lot; that means the uniform width of the lawn is 90/2 = 45 feet.
Answer by MathTherapy(10549)  (Show Source):
You can put this solution on YOUR website!
A factory is to be built on a lot measuring 270 ft by 360 ft. A local building code specifies that a lawn of uniform width and equal in area to the factory must surround the factory.
What must the width of the lawn be? ?
If the dimensions of the factory are A ft by B ft with A
and B= ?
Let uniform width of lawn be x
Then dimensions of factory are 270 - 2x and 360 - 2x, and its area is: (270 - 2x)(360 - 2x)
2[(270 - 2x)(360 - 2x)] = 270(360)
2[2(135 - x)2(180 - x)] = 2(135)(4)(90)
8(135 - x)(180 - x) = 8(135)(90)
(135 - x)(180 - x) = 135(90)
x(x - 270) - 45(x - 270) = 0
x - 45 = 0 or x - 270 = 0
Uniform width, or  or x = 270 (ignore)
|
|
|
