Question 118549: please help me solve 3X<6
Found 2 solutions by tutor_paul, solver91311:
Answer by tutor_paul(519)   (Show Source): (Show Source):
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solve inequalities just like you do equations, that is to say you add equal quantities to both sides, multiply both sides by equal quantitities, or raise both sides to a power to manipulate the statement so that you have just the variable on one side of the relationship symbol and everything else, reduced to simplest terms, on the other side. But there is one very important exception. If you multiply by a negative number, you must reverse the sense of the inequality in the process.
For your problem:  , just multiply both sides by , just multiply both sides by  resulting in resulting in  . That means that the solution set is all real numbers on the interval . That means that the solution set is all real numbers on the interval 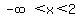 . Note that the number 2 is NOT included in that interval. . Note that the number 2 is NOT included in that interval.
Here's what it looks like on a number line:

Let's look at some examples: First choose a value inside of the specified interval, 1 for example. 3 times 1 is 3 and that is less than 6. Now let's pick another value outside of the interval, 3 for example. 3 times 3 is 9 and that is definitely NOT less than 6. It is also interesting to look at the endpoint of the interval, in this case 2. 3 times 2 is 6, and 6 is equal to 6 -- NOT less than 6, whereas 3 times 1.99999999999999 is 5.99999999999997
and that IS less than 6, though not very much less.
The one concept you need to embrace when dealing with linear inequalities is that the solution set has an infinite number of elements, except for situations where there is no solution at all. This is in contrast to a linear equation in one variable which has exactly one element in its solution set. From the beginning of your education in mathematics you have been used to dealing with problems that had exactly one answer, so the idea that there could be more than one answer, much less an infinite number of answers, is sometimes hard to swallow.
By contrast, let's say that your problem was actually 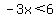 . In this case you would multiply both sides of the inequality by . In this case you would multiply both sides of the inequality by  . But since you are multiplying by a negative number, you have to reverse the sense of the inequality (less than (<) becomes greater than (>)). Therefore your result would be . But since you are multiplying by a negative number, you have to reverse the sense of the inequality (less than (<) becomes greater than (>)). Therefore your result would be  , solution set being any real number in the interval , solution set being any real number in the interval 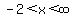 . .
Super-Double-Plus Extra Credit.
How many real numbers are there in the interval 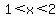 ? ?
How about in the interval 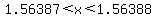 ? ?
How many rational numbers are in these two intervals?
How many irrational numbers are in these two intervals?
Extra-Special-Super-Double-Plus Extra Credit.
Why, in the initial paragraph above, did I only mention addition, multiplication, and raising to a power -- what happened to subtraction, division, and taking a root?
Hope this helps,
John
|
|
|