Question 1185416: You just sold a house for $200,000. You can invest the money at 5%/a compounded semiannually. How much could you withdraw every 6 months, starting in 6 months, for the next 20 years?
Answer by ikleyn(52873)   (Show Source):
You can put this solution on YOUR website! .
You just sold a house for $200,000. You can invest the money at 5%/a compounded semiannually.
How much could you withdraw every 6 months, starting in 6 months, for the next 20 years?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This problem is about a sinking fund.
The starting amount is A = $200,000.
The fund is compounded semi-annually at the annual compounding rate r = 5%.
You want to withdraw a regular amount at the end of each 6 months period during next 20 years.
They want you determine the value of this regular withdraw amount W.
Use the formula for a sinking fund
A =  , (1)
where A is the starting amount, W is the regular withdraw amount semi-annually,
r is the annual compounding rate, m is the number of withdrawals per year (m= 2 in this problem),
n is the total number of withdrawals/compounding (twice the number of years, in this problem),
 is the effective rate of compounding per the 6 months period.
With the given data, formula (1) takes the form
200000 = 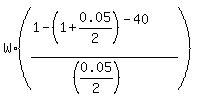 =  = W*25.102775 dollars.
From this equation, we find the semiannual withdraw value
W =  = 7967.25 dollars.
ANSWER. The semi-annual withdrawal value is $7967.25.
Solved.
|
|
|
