|
Question 1185345: Find the area of a quadrilateral having the points (-3, 4), (-2, -1), (4, 4) and (0, 5)
as vertices.
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! Find the area of a quadrilateral having the points A(-3,4), B(-2,-1), C(4,4) and D(0,5) as vertices.
-------------------
A B C D A
-3 -2 4 0 -3
4 -1 4 5 4
--------------
Add the diagonal products starting at the upper left.
--> 3 -8 +20 + 0 = 15
----
Add the diagonal products starting at the lower left.
--> -8 -4 + 0 -15 = -27
The difference is 42.
The area is 1/2 that = 21 sq units.
Answer by ikleyn(52794)  (Show Source):
You can put this solution on YOUR website! .
Find the area of a quadrilateral having the points A(-3, 4), B(-2, -1), C(4, 4) and D(0, 5).
~~~~~~~~~~~~~~~~~
I will assume that the vertices of the quadrilateral go in that order as the points are listed.
Then I see that the diagonal AC of the quadrilateral is horizontal y=4 and divides the quadrilateral in two triangles.
Triangle ABC has the vertex B BELOW the diagonal line y= 4.
It has the base AC of the length 4 - (-3) = 7 units and the altitude drawn to AC of the length 4 - (-1) = 5 units.
Hence, the area of the triangle ABC is 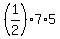 = 17.5 square units.
Next, triangle ADC has the vertex D ABOVE the diagonal line y= 4.
It has the base AC of the length 4 - (-3) = 7 units and the altitude drawn to AC of the length 5 - 4 = 1 units.
Hence, the area of the triangle ADC is 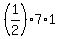 = 3.5 square units.
Finally, the area of the quadrilateral ABCD is the sum of the areas of the triangles ABC and ADC
 = 17.5 + 3.5 = 21 square units. ANSWER
Solved.
/////////////
How Alan solved the problem, it assumes that the reader knows EVERYTHING in Geometry, including Analytic Geometry.
In my view, it is absolutely unrealistic hypothesis.
Much more closer to reality is to assume that the reader knows NOTHING except the basic knowledge.
So I adapted my solution correspondingly.
|
|
|
| |
