SOLUTION: I am a rational function having a vertical asymptote at the lines x = 3 and x = -3, and a horizontal asymptote at y = 1 . If my only x-intercept is 5, and my y-intercept

Algebra ->  Rational-functions -> SOLUTION: I am a rational function having a vertical asymptote at the lines x = 3 and x = -3, and a horizontal asymptote at y = 1 . If my only x-intercept is 5, and my y-intercept       Log On


   

Question 1185294: I am a rational
function having a vertical asymptote at
the lines x = 3 and x = -3, and a
horizontal asymptote at y = 1 . If my
only x-intercept is 5, and my y-intercept
is - 5/9 , what function am I?
Found 2 solutions by greenestamps, Edwin McCravy:
Answer by greenestamps(13203) About Me  (Show Source):
You can put this solution on YOUR website!


The conditions are over-specified; there is no rational function that satisfies all the conditions....

(1) vertical asymptotes at x=3 and x=-3:

This means there must be factor(s) of (x-3) and (x+3) in the denominator; and no other linear factors

r%28x%29=a%2F%28%28%28x-3%29%5Em%29%28%28x%2B3%29%5En%29%29

(2) horizontal asymptote at y=1:

This means the leading terms of the numerator and denominator are the same (same coefficient and same power). That means the coefficient a is 1, and the number of linear factors is the same in numerator and denominator.

r%28x%29=1%2F%28%28%28x-3%29%5Em%29%28%28x%2B3%29%5En%29%29

(3) only x-intercept at x=5:

The only factor(s) in the numerator are (x-5). From (2), the total number of linear factors in the numerator and denominator must be the same

r%28x%29=%28x-5%29%5E%28m%2Bn%29%2F%28%28%28x-3%29%5Em%29%28%28x%2B3%29%5En%29%29

(4) y-intercept -5/9:

Set x=0 and see what happens

r%280%29=%28-5%29%5E%28m%2Bn%29%2F%28%28%28-3%29%5Em%29%28%283%29%5En%29%29=-5%2F9

Ignoring signs, with only factors of 5 in the numerator and only factors of 3 in the denominator, the only way to get a y-intercept of 5/9 is with one factor of 5 in the numerator and two factors of 3 in the denominator. But that would make the function

r%28x%29=%28x-5%29%2F%28%28x-3%29%28x%2B3%29%29

And that has both the wrong y-intercept (5/9 instead of -5/9) and the wrong horizontal asymptote (y=0 instead of y=1).

ANSWER: There is no rational function with all the prescribed conditions

Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
Greenestamps didn't think of the sneaky trick of eliminating an x-intercept by
putting an extra factor in the numerator and denominator to create a hole in the
curve instead of having an x-intercept.  I'll use that trick.

To have those vertical asymptotes, the denominator, when set = 0, must have
roots 3 and -3, so the denominator must contain (x-3)(x+3), which has degree 2
and leading coefficient 1.  That might be enough for the denominator.  If so,
the numerator must also be of degree 2 and have leading coefficient 1 in order
to have horizontal asymptote y = 1.  So let's try this version:

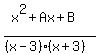y%22%22=%22%22%28x%5E2%2BAx%2BB%29%2F%28%28x-3%29%28x%2B3%29%29

To have x-intercept 5, it must go through (5,0).  So we substitute 

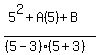
0%22%22=%22%22%285%5E2%2BA%285%29%2BB%29%2F%28%285-3%29%285%2B3%29%29

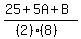0%22%22=%22%22%2825%2B5A%2BB%29%2F%28%282%29%288%29%29

Multiply through by 16

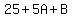
0%22%22=%22%2225%2B5A%2BB

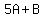5A%2BB%22%22=%22%22-25

To have y-intercept -5/9, it must go through (0,-5/9).  So we substitute 

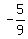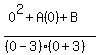
-5%2F9%22%22=%22%22%280%5E2%2BA%280%29%2BB%29%2F%28%280-3%29%280%2B3%29%29

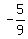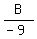-5%2F9%22%22=%22%22B%2F%28-9%29

Multiply both sides by -9

5%22%22=%22%22B

Substituting in

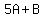
5A%2BB%22%22=%22%22-25
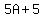
5A%2B5%22%22=%22%22-25
5A%22%22=%22%22-30
A%22%22=%22%22-6

So let's substitute those values for A and B in

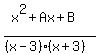
y%22%22=%22%22%28x%5E2%2BAx%2BB%29%2F%28%28x-3%29%28x%2B3%29%29

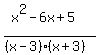y%22%22=%22%22%28x%5E2-6x%2B5%29%2F%28%28x-3%29%28x%2B3%29%29

Let's graph it and see what we have:



Oh darn! That has an extra x-intercept at (1,0).  Aha, but I can play the trick!
I'll put a hole in the curve at (1,0) by putting in a factor of (x-1) in
the numerator and the denominator:

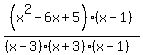y%22%22=%22%22%28x%5E2-6x%2B5%29%28x-1%29%2F%28%28x-3%29%28x%2B3%29%28x-1%29%29

Then the graph has a hole at (1,0) instead of an x-intercept there.



The un-factored form of the rational function is:

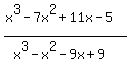y%22%22=%22%22%28x%5E3-7x%5E2%2B11x-5%29%2F%28x%5E3-x%5E2-9x%2B9%29

Edwin