|
Question 1185283: Find the coordinates of the center, vertices, foci and equation of the asymptotes of the following hyperbolas:
a. 36x2 - 25y2 - 72x + 50y - 889 = 0
b. x2 - 4y2 - x + 12y = 0
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
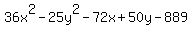   Swap the middle two terms to get like lettered terms together:
Swap the middle two terms to get like lettered terms together:
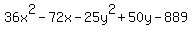   Factor 36 out of the two terms in x: (Factor out 36, not 36x)
Factor 36 out of the two terms in x: (Factor out 36, not 36x)
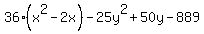   Factor -25 out of the two terms in y: (Factor out -25, not -25y)
Factor -25 out of the two terms in y: (Factor out -25, not -25y)
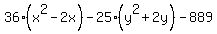   Add 889 to both sides:
Add 889 to both sides:
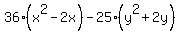  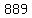 Complete the square inside the first parentheses:
1. To the side, multiply the coefficient of x, which is -2, by 1/2, getting -1.
2. Square this value, get +1
3. Add then subtract it "+1-1" inside the first parentheses
Complete the square inside the first parentheses:
1. To the side, multiply the coefficient of x, which is -2, by 1/2, getting -1.
2. Square this value, get +1
3. Add then subtract it "+1-1" inside the first parentheses
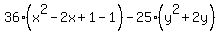  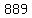 Complete the square inside the second parentheses:
1. To the side, multiply the coefficient of y, which is -2, by 1/2, getting -1.
2. Square this value, get +1
3. Add then subtract it "+1-1" inside the second parentheses
Complete the square inside the second parentheses:
1. To the side, multiply the coefficient of y, which is -2, by 1/2, getting -1.
2. Square this value, get +1
3. Add then subtract it "+1-1" inside the second parentheses
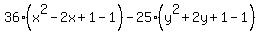  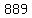 Factor the first three terms inside the first parentheses using a large
parentheses with small parentheses inside:
Factor the first three terms inside the first parentheses using a large
parentheses with small parentheses inside:
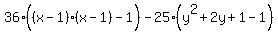  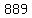 Factor the first three terms inside the second parentheses using a large
parentheses with small parentheses inside:
Factor the first three terms inside the second parentheses using a large
parentheses with small parentheses inside:
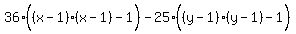  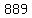 Write the products of binomials with themselves as the square of one
binomial:
Write the products of binomials with themselves as the square of one
binomial:
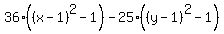  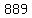 Remove the larger parentheses by distributing, leaving the smaller
parentheses intact:
Remove the larger parentheses by distributing, leaving the smaller
parentheses intact:
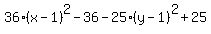  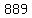 Combine the two constant terms on the left
Combine the two constant terms on the left
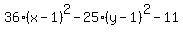  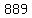 Add 11 to both sides
Add 11 to both sides
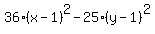   Divide each term on both sides by 900 to make the right side become 1:
Divide each term on both sides by 900 to make the right side become 1:
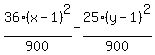   Divide the numerators and denominators by the coefficients on top:
Divide the numerators and denominators by the coefficients on top:
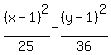   Compare this to
Compare this to
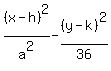   and we see that
h=1, k=1, a2=25, a=5, b2=36, b=6.
The center is (h,k) = (1,1).
We plot the center. We draw the transverse axis which is a=5 units on both
sides of the center. Then we draw the conjugate axis which is b=6 units vertically above and below the center.
and we see that
h=1, k=1, a2=25, a=5, b2=36, b=6.
The center is (h,k) = (1,1).
We plot the center. We draw the transverse axis which is a=5 units on both
sides of the center. Then we draw the conjugate axis which is b=6 units vertically above and below the center.
 We draw the defining rectangle so that the two axes bisect it:
We draw the defining rectangle so that the two axes bisect it:
 We draw and extend the two diagonals of the defining rectangle, which are the
asymptotes of the hyperbola:
We draw and extend the two diagonals of the defining rectangle, which are the
asymptotes of the hyperbola:
 Now we sketch in the hyperbola:
Now we sketch in the hyperbola:
 The center is (1,1)
The vertices are (-4,1) and (6,1)
To find the foci, we use the Pythagorean formula
to find their distance from the center
The center is (1,1)
The vertices are (-4,1) and (6,1)
To find the foci, we use the Pythagorean formula
to find their distance from the center
  
  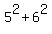
  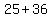
  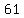
   That is added to and subtracted from the x coordinate of the center to get
the coordinates of the foci. The foci are on the extension of the transverse
axes, shown below, and have the coordinates:
That is added to and subtracted from the x coordinate of the center to get
the coordinates of the foci. The foci are on the extension of the transverse
axes, shown below, and have the coordinates:

 Edwin
Edwin
|
|
|
| |