|
Question 1185110: Jenny had 3/5 as many beads as Kelly. Kelly gave Jenny 24 beads. Then, Jenny had  of all the beads. How many beads did they have?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52898)   (Show Source):
You can put this solution on YOUR website! .
Jenny had 3/5 as many beads as Kelly. Kelly gave Jenny 24 beads.
Then, Jenny had 3/4 of all the beads. How many beads did they have  ?
~~~~~~~~~~~~~~~
After reading the post, I do not understand the problem's question.
How many beads did they have TOGETHER ? SEPARATELY ?
If SEPARATELY, then AT THE BEGINNING or AT THE END ?
In this sense, the post is DEFECTIVE (and deserves serious punishment).
In order for it would make sense, I will consider the question in this form:
How many beads did EACH of THEM have AT THE BEGINNING ?
Since "Jenny had 3/5 as many beads as Kelly", we can think that Kelly had 5x beads, while Jenny had 3x beads.
After Kelly gave Jenny 24 beads, they have: Kelly 5x-24 beads; Jenny 3x+24 beads.
The total beads is 5x + 3x = 8x.
The last condition of the problem states that
3x + 24 =  .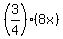
Simplify this equation and find x
3x + 24 = 3*(2x)
3x + 24 = 6x
24 = 6x - 3x
24 = 3x
x = 24/3 = 8.
ANSWER. Originally, they had 8*5 = 40 beans (Kelly) and 8*3 = 24 beans (Jenny).
If you want to know the total, you may add these numbers.
Solved and thoroughly explained.
Answer by greenestamps(13214)  (Show Source):
|
|
|
| |
