Question 1185100: A normal distribution has a mean of 20 and a standard deviation of 10. Two scores are sampled randomly from the distribution and the second score is subtracted from the first. What is the probability that the difference score will be greater than 5? Hint: Read the Variance Sum Law section of Chapter 3.
Found 2 solutions by ikleyn, robertb:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A normal distribution has a mean of 20 and a standard deviation of 10. Two scores are sampled randomly
from the distribution and the second score is subtracted from the first. What is the probability
that the difference score will be greater than 5?
Hint: Read the Variance Sum Law section of Chapter 3.
~~~~~~~~~~~~~~~~~
I can not use this hint, since I have no this textbook, which you, probably/perhaps, have.
So, you are in much better position than me to answer this question.
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! It is a result in statistics, which you should also be aware of because you were given this kind of problem,
that if X ~ N(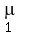 , , 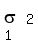 ) and Y ~ N( ) and Y ~ N(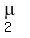 , , 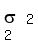 ), and X and Y are independent from each other, then ), and X and Y are independent from each other, then
X - Y ~ N(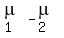 , , 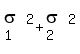 ). ).
Since the two scores were sampled randomly from the same population, the scores are independent from each other, and so
X - Y ~ N(0,  ) )
===> 
Normal probabilities were taken from https://stattrek.com/online-calculator/normal.aspx.
|
|
|