Question 1185098: A six-sided die is printed with the numbers 1,2,3,5,8 and 13. Roll the dice
once- what is the probability of getting an even number?
roll the die twice and add the numbers; what is the probability of getting
an odd sum?
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! A six-sided die is printed with the numbers 1,2,3,5,8 and 13. Roll the
dice once- what is the probability of getting an even number?
1, 2, 3, 5, 8, 13
Count the red ones, get 2. Count them all, get 6. That's a probability of
2 out of 6, or 2/6, which reduces to 1/3.
roll the die twice and add the numbers; what is the probability of getting
an odd sum?
(1,1) (1,2) (1,3) (1,5) (1,8) (1,13)
(2,1) (2,2) (2,3) (2,5) (2,8) (2,13)
(3,1) (3,2) (3,3) (3,5) (3,8) (3,13)
(5,1) (5,2) (5,3) (5,5) (5,8) (5,13)
(8,1) (8,2) (8,3) (8,5) (8,8) (8,13)
(13,1) (13,2) (13,3) (13,5) (13,8) (13,13)
Count the red ones, get 16. Count them all, get 36. That's a probability of
16 out of 36, or 16/36, which reduces to 4/9.
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! A six-sided die is printed with the numbers 1,2,3,5,8 and 13.
(a) Roll the dice once- what is the probability of getting an even number?
(b) roll the die twice and add the numbers; what is the probability of getting
an odd sum?
~~~~~~~~~~~~~~~~
(a) The probability is the ratio of favorable outputs to the total outputs.
In question (a), there are 2 favorable outputs against 6 total outputs.
You can do the rest.
(b) In case (b), the total number of all possible outputs is 6*6 = 36.
Of them, favorable are sums of even and odd outputs, and the number of such outputs (pairs) is 2*4 + 4*2 = 16.
So, the number of total favorable outputs is 16 against total possible outputs 36.
THEREFORE, the probability in case (b) is P = 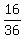 = =  . .
Solved.
---------------
An idea which I want to deliver to you in my post is THIS:
To answer question (b), it is not necessary to calculate all, each and every of 36 possible outputs individually and separately.
You can evaluate all necessary numbers for the solution in more simple and cheaper way, spending less efforts.
|
|
|