Question 1185076: The Halloween Express is making pre-packaged bags of candy for customers to give out to trick-or-treaters. The store has 20 tootsie rolls and 18 suckers. Package A requires 1 tootsie roll and 3 suckers. Package B requires 5 tootsie rolls and 1 sucker. If package A sells for $2 and package B sells for $3, how many of each package should they make to maximize profit?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Not enough information....
Profit can't be maximized knowing only the sales price; we also need to know the cost.
Re-post with all the required information.
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The Halloween Express is making pre-packaged bags of candy for customers to give out to trick-or-treaters.
The store has 20 tootsie rolls and 18 suckers.
Package A requires 1 tootsie roll and 3 suckers.
Package B requires 5 tootsie rolls and 1 sucker.
If package A sells for $2 and package B sells for $3, how many of each package should they make to maximize 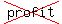 revenue ? revenue ?
~~~~~~~~~~~~~~~~~~
It is quite obvious, that at the given circumstances, the problem's question
should be about the REVENUE and not about the profit.
With this editing, see my solution below.
Let X be the number of packages A and Y be the number of packages B.
Then we want maximize the revenue function
R(X,Y) = 2X + 3Y
under the following restrictions
X + 5Y <= 20 (toorsie rolls)
3X + Y <= 18 (suckers)
X >= 0, Y >= 0
The plot of the feasibility domain is shown in the Figure below.
 Plots y =
Plots y = 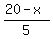 (red) and y = 18-3x (green)
It is a quadrilateral in QI with the vertices (X,Y) = (0,0), (0,4), (5,3), (6,0).
We apply the standard Linear Programming method in its geometric interpretation.
The solution is one of these 4 points, where the objective function (profit) has a maximum.
You calculate the values of the objective function R(X,Y) (revenue) at listed points
P(0,0) = 2*0 + 3*0 = 0
P(0,4) = 2*0 + 3*4 = 12
P(5,3) = 2*5 + 3*3 = 19
P(6,0) = 2*6 + 3*0 = 12.
Comparing these values, you find the optimal point.
It is (X,Y) = (5,3), which means 5 boxes A and 3 boxes B, providing maximum REVENUE of 19 dollars. (red) and y = 18-3x (green)
It is a quadrilateral in QI with the vertices (X,Y) = (0,0), (0,4), (5,3), (6,0).
We apply the standard Linear Programming method in its geometric interpretation.
The solution is one of these 4 points, where the objective function (profit) has a maximum.
You calculate the values of the objective function R(X,Y) (revenue) at listed points
P(0,0) = 2*0 + 3*0 = 0
P(0,4) = 2*0 + 3*4 = 12
P(5,3) = 2*5 + 3*3 = 19
P(6,0) = 2*6 + 3*0 = 12.
Comparing these values, you find the optimal point.
It is (X,Y) = (5,3), which means 5 boxes A and 3 boxes B, providing maximum REVENUE of 19 dollars.
Solved.
--------------
In this site, there is a lesson
- Solving minimax problems by the Linear Programming method
which explains, for beginners, metodology of solving such problems in more details.
|
|
|